Table of Contents
- Introduction
- Home Heating and Cooling Fundamentals
- Understanding Thermal Inertia
- Dynamic Home Heating and Cooling with Thermal Inertia
- Algorithm: Dynamic Home Heating and Cooling with Thermal Inertia
- Conclusion
- Algorithm to Implement Dynamic Home Heating and Cooling with Thermal Inertia
Introduction
Thermal inertia is one of the most critical yet often overlooked factors influencing the energy efficiency and comfort of modern homes. It plays a pivotal role in how buildings interact with their surrounding environment, determining how quickly they respond to temperature changes and how effectively they retain heat or coolness. In an era where energy efficiency, sustainability, and smart home technologies are becoming increasingly important, understanding and leveraging thermal inertia has never been more relevant.
This comprehensive guide explores the scientific principles, practical applications, and technological integrations of thermal inertia in home climate control systems. By delving into the nuances of material properties, building design, and cutting-edge HVAC optimization techniques, it provides homeowners, builders, and automation enthusiasts with actionable insights to reduce energy consumption and enhance indoor comfort.
The Importance of Thermal Inertia in Energy Efficiency
The concept of thermal inertia refers to a material’s ability to absorb, store, and release heat over time. Buildings with high thermal inertia can moderate indoor temperature fluctuations by storing heat during warm periods and releasing it when temperatures drop. This passive regulation not only reduces the reliance on active heating or cooling systems but also contributes to significant energy savings and improved thermal comfort.
Thermal inertia is particularly valuable in climates with significant diurnal temperature variations. For example:
- In hot, sunny regions, high thermal mass materials like concrete or stone can absorb heat during the day and release it at night, reducing the need for air conditioning.
- In colder climates, thermal inertia can help maintain warmth overnight, reducing the strain on heating systems.
By integrating thermal inertia into the design of homes and HVAC systems, it is possible to create energy-efficient environments that adapt seamlessly to changing weather conditions.
Bridging Science and Technology: Thermal Inertia in Smart Homes
As smart home technologies become increasingly sophisticated, thermal inertia is emerging as a crucial factor in automated climate control systems. Smart thermostats, predictive algorithms, and adaptive HVAC systems now allow homeowners to harness the benefits of thermal inertia effectively. These systems use real-time data from sensors to anticipate temperature changes, optimize heating or cooling schedules, and minimize energy waste.
For instance, smart thermostats can:
- Adjust pre-heating or pre-cooling schedules based on the thermal lag of materials, ensuring that the desired indoor temperature is reached at the right time.
- Integrate weather forecast data to anticipate temperature fluctuations and modify HVAC operations accordingly.
- Use machine learning algorithms to analyze occupancy patterns, outdoor conditions, and thermal inertia properties for continuous optimization.
This integration of thermal inertia with smart technology represents a paradigm shift in home climate control, enabling homeowners to achieve unparalleled energy efficiency while maintaining comfort.
Scope and Structure of the Guide
This guide provides an in-depth exploration of thermal inertia, focusing on its applications in energy-efficient home design and smart climate control systems. It is divided into several sections that collectively address the scientific, practical, and technological aspects of the topic:
- Understanding Thermal Inertia:
- Introduces the fundamental principles of thermal inertia and its impact on energy efficiency and thermal comfort.
- Discusses the thermal properties of various building materials, including their density, specific heat capacity, and thermal conductivity.
- Applications in Smart Thermostats:
- Explores how thermal inertia can be integrated into adaptive scheduling algorithms for HVAC systems.
- Provides detailed guidance on sensor placement, material selection, and real-time data integration.
- Predictive Heating and Cooling:
- Examines the role of thermal inertia in predictive HVAC systems, including the use of weather forecasts and real-time adjustments to optimize energy use.
- Advanced Control Strategies:
- Focuses on advanced algorithms like Proportional-Integral-Derivative (PID) control and machine learning, demonstrating how they can be used to leverage thermal inertia in smart home systems.
- Quantifying Energy Savings:
- Provides methodologies for calculating energy savings achieved through the integration of thermal inertia, including real-world examples and comparative analyses.
- Practical Implementation:
- Offers actionable recommendations for homeowners and developers, from selecting the right materials to setting up sensors and integrating smart technologies.
Who Can Benefit from This Guide?
This guide is designed for a wide audience, including:
- Homeowners: Seeking ways to reduce energy bills and create comfortable living spaces through efficient heating and cooling.
- Builders and Architects: Interested in incorporating thermal inertia principles into sustainable building designs.
- Smart Home Enthusiasts: Looking to optimize their automated climate control systems with advanced algorithms and predictive models.
- Researchers and Engineers: Exploring the intersection of thermal physics, material science, and smart technology.
Key Takeaways
By the end of this guide, readers will:
- Understand the science behind thermal inertia and its practical implications for energy efficiency.
- Learn how to optimize home climate control systems by leveraging the thermal properties of building materials.
- Gain insights into integrating smart technology with thermal inertia for maximum efficiency and comfort.
- Be equipped with tools, equations, and Python code for real-world implementation and analysis.
Thermal inertia is more than just a scientific concept. It is a powerful tool for transforming homes into energy-efficient, sustainable, and smart living spaces. This guide serves as a roadmap for unlocking its full potential.
1. Introduction to Thermal Inertia in Buildings
The concept of thermal inertia is fundamental in building design and plays a significant role in climate control, energy efficiency, and comfort within built environments. Thermal inertia describes the capacity of building materials to resist changes in temperature, impacting how indoor environments respond to external weather fluctuations and contributing to overall energy efficiency. This section delves into the core definitions, importance for comfort, energy efficiency benefits, and practical applications of thermal inertia, particularly in home automation contexts.
- 1.1 Definition and Key Concepts
- 1.1.1 Thermal Inertia Explained
Thermal inertia is defined as a material’s resistance to changes in temperature. Unlike thermal conductivity, which focuses on the rate at which heat passes through a material, thermal inertia encompasses a material’s ability to absorb, store, and slowly release heat. This attribute is particularly beneficial in climates with significant temperature variations, as materials with high thermal inertia can buffer these fluctuations, reducing the need for mechanical heating and cooling. The thermal inertia of a building material is influenced by its specific heat capacity, density, and thermal conductivity. Dense materials like concrete, brick, and stone have higher thermal inertia than lighter materials, enabling them to store heat for extended periods and release it slowly. This delayed response helps maintain a stable indoor climate, as these materials gradually release the heat they have absorbed, balancing indoor temperatures even when outdoor temperatures fluctuate. - 1.1.2 Distinguishing Thermal Inertia from Thermal Conductivity
While thermal inertia and thermal conductivity are often discussed together, they refer to distinct properties. Thermal conductivity measures how quickly heat moves through a material, with high thermal conductivity indicating fast heat transfer, as seen in metals. Thermal inertia, on the other hand, focuses on a material’s ability to retain heat over time, providing a “thermal buffer” effect. This distinction is critical in building design, where materials are selected not only for their insulation properties but also for their ability to modulate indoor temperatures in response to changing outdoor conditions. Understanding these differences allows architects and engineers to choose materials that complement the building’s climate control strategy. For example, in hot climates, low thermal conductivity materials are paired with high thermal inertia to prevent rapid heat entry while still storing any absorbed heat for gradual release. Reference: Santamouris, M. (2019). Cooling Energy Solutions for Buildings and Cities. Elsevier.
- 1.1.1 Thermal Inertia Explained
- 1.2 Importance of Thermal Inertia for Indoor Comfort
- 1.2.1 Temperature Stability and Human Comfort
Thermal inertia contributes significantly to maintaining stable indoor temperatures, which is crucial for human comfort. Temperature stability prevents drastic fluctuations that can lead to discomfort, fatigue, and, in some cases, health issues. High thermal inertia materials absorb excess heat during the day and gradually release it at night, ensuring a balanced indoor environment that reduces reliance on heating and cooling systems. This characteristic of thermal inertia promotes a steady climate within buildings, which is especially beneficial in spaces where thermal comfort is essential, such as residential homes, offices, and schools. - 1.2.2 Reducing Temperature Swings
Thermal inertia acts as a buffer against sudden outdoor temperature changes, absorbing and retaining heat energy. This “thermal lag” effect is beneficial in both hot and cold climates, as it minimizes the impact of abrupt weather changes, protecting the interior environment from extreme temperatures. For example, in desert climates where daytime and nighttime temperatures vary widely, buildings with high thermal inertia can absorb daytime heat and release it during cooler nights, making it easier to maintain comfortable indoor temperatures without excessive HVAC use. Reference: Givoni, B. (1994). Passive and Low Energy Cooling of Buildings. John Wiley & Sons.
- 1.2.1 Temperature Stability and Human Comfort
- 1.3 How Thermal Inertia Relates to Energy Efficiency
- 1.3.1 Lowering Energy Demand with Thermal Inertia
One of the primary benefits of thermal inertia is its potential to lower energy consumption by reducing the frequency and intensity of HVAC operation. High thermal inertia buildings experience slower temperature changes, lessening the need for mechanical heating and cooling. By maintaining a more consistent indoor temperature, thermal inertia can reduce the workload on HVAC systems, leading to significant energy savings over time. This advantage aligns with growing sustainability goals and energy efficiency standards, as less energy demand means lower greenhouse gas emissions and cost savings for homeowners. - 1.3.2 Environmental Impact of Reduced Energy Consumption
Reducing energy demand has a positive environmental impact by decreasing the carbon footprint associated with heating and cooling buildings. Thermal inertia supports passive climate control, which lessens dependence on fossil fuels and reduces greenhouse gas emissions. Furthermore, utilizing materials with high thermal inertia in building designs supports sustainable practices by enabling passive heating and cooling solutions, which are essential in addressing climate change and promoting green building practices. Reference: Santamouris, M., & Kolokotsa, D. (2013). “Passive cooling dissipation techniques for buildings and other structures.” Energy and Buildings, Elsevier.
- 1.3.1 Lowering Energy Demand with Thermal Inertia
- 1.4 Practical Applications of Thermal Inertia in Home Automation
- 1.4.1 Algorithm for Calculating Effective Thermal Mass (ETM)
In modern smart homes, thermal inertia data can be leveraged to optimize HVAC scheduling and enhance energy efficiency. An algorithm to calculate Effective Thermal Mass (ETM) allows home automation systems to estimate a building’s thermal storage capacity based on material properties, room dimensions, and exposure to sunlight. By incorporating this algorithm into smart thermostats or building management systems, homes can preemptively adjust HVAC settings based on expected heat retention or dissipation, improving both comfort and efficiency. - 1.4.2 Simulating Thermal Response Time for HVAC Systems
Another practical application involves simulating the thermal response time of a building to predict how long it will retain heat or cool air. Using basic heat transfer equations, smart HVAC systems can simulate how quickly different parts of a building will respond to temperature changes. This predictive model allows the system to make anticipatory adjustments, like pre-cooling or pre-heating rooms, which can further optimize energy usage and reduce strain on HVAC components. Reference: Santamouris, M. (2019). Cooling Energy Solutions for Buildings and Cities. Elsevier.
- 1.4.1 Algorithm for Calculating Effective Thermal Mass (ETM)
2. How Thermal Mass Contributes to Thermal Inertia
Thermal mass is a critical component in understanding thermal inertia, as it enables materials to absorb, store, and gradually release heat, directly influencing a building’s temperature stability. The effectiveness of thermal mass in building design is largely determined by material choice, structure, and placement. This section explores the role of thermal mass in various building elements, the types of materials with high thermal mass, and their impact on heating and cooling.
- 2.1 Defining Thermal Mass and Its Role in Buildings
- 2.1.1 What is Thermal Mass?
Thermal mass refers to a material’s capacity to absorb, store, and release heat. Unlike insulation, which prevents heat transfer, thermal mass acts as a “thermal battery,” storing heat during warmer periods and releasing it when temperatures cool. This property enables buildings to maintain a stable internal environment, reducing reliance on active heating and cooling systems. Thermal mass is particularly beneficial in climates with high diurnal temperature variations, as it helps smooth out daily temperature swings by delaying heat transfer. - 2.1.2 Thermal Mass in Walls, Floors, and Ceilings
The building envelope (walls, floors, and ceilings) plays a significant role in thermal mass storage. Materials like concrete, brick, stone, and even water can serve as thermal mass in these components. For instance:- Walls: Walls constructed with high thermal mass materials can absorb solar heat throughout the day and release it slowly at night, reducing heating demands during colder periods.
- Floors: Thermal mass floors, often made from concrete or stone, absorb sunlight directly from windows and store it, acting as a thermal buffer that radiates warmth during the evening.
- Ceilings: Less common but effective in some designs, thermal mass ceilings can store excess heat, particularly in multi-story buildings where heat rises and accumulates at higher levels.
- 2.1.1 What is Thermal Mass?
- 2.2 Types of Materials with High Thermal Mass
- 2.2.1 Concrete and Brick
Concrete and brick are among the most commonly used high thermal mass materials. Their high density and specific heat capacity enable them to store substantial amounts of heat. Concrete, due to its durability and versatility, is frequently used in floors and walls, particularly in passive solar building designs where its thermal mass can be maximized. Brick, while less dense than concrete, offers a similar benefit and is often used in load-bearing walls that also function as thermal mass reservoirs. The combination of these materials in construction contributes to effective temperature moderation, reducing the load on HVAC systems. - 2.2.2 Water and Phase Change Materials (PCMs)
Water is an excellent medium for thermal storage because of its high specific heat capacity, making it capable of absorbing large quantities of heat relative to its mass. In passive solar designs, water can be stored in containers that receive direct sunlight, absorbing heat during the day and releasing it slowly at night. Phase change materials (PCMs) are advanced materials engineered to absorb and release heat at specific temperatures. PCMs store heat when they change from solid to liquid and release it as they solidify. They are highly effective in maintaining stable indoor temperatures and are increasingly integrated into building systems, such as wall panels or ceiling tiles, to enhance thermal inertia. Reference: Al-Homoud, M. S. (2005). “Performance characteristics and practical applications of common building thermal insulation materials.” Building and Environment, Elsevier.
- 2.2.1 Concrete and Brick
- 2.3 Impact of Thermal Mass on Heating and Cooling
- 2.3.1 Heat Absorption and Release
Thermal mass materials absorb heat during warmer hours and release it when temperatures drop, a process governed by the material’s thermal conductivity and specific heat capacity. This cycle of heat absorption and release helps reduce temperature fluctuations within buildings. During winter, thermal mass absorbs indoor heat generated by sunlight or heaters, storing it and releasing it slowly to keep interiors warm at night. In summer, the thermal mass absorbs excess indoor heat, reducing cooling demands. The timing of heat release, known as “thermal lag,” is crucial in passive building designs and can be optimized by strategically choosing and placing high thermal mass materials. - 2.3.2 Passive Heating and Cooling
Passive heating and cooling leverage thermal mass to maintain comfortable indoor temperatures without relying heavily on mechanical HVAC systems. By capturing solar heat during the day and releasing it as temperatures drop, thermal mass reduces the need for active heating at night. Similarly, thermal mass absorbs and buffers against peak daytime heat in summer, contributing to passive cooling by preventing indoor temperatures from rising rapidly. Integrating thermal mass in building envelopes allows designers to minimize HVAC energy consumption and achieve a more stable indoor climate, often considered essential in sustainable building practices. Reference: Givoni, B. (1994). Passive and Low Energy Cooling of Buildings. John Wiley & Sons.
- 2.3.1 Heat Absorption and Release
- 2.4 The Impact of Building Materials on Thermal Inertia
- 2.4.1 Insulating vs. Conductive Materials
While thermal mass materials are valued for their ability to store heat, insulation plays a different but complementary role. Insulating materials, such as fiberglass, foam, and cellulose, prevent heat transfer, keeping indoor environments thermally isolated from outdoor conditions. For optimal thermal inertia, a combination of thermal mass and insulation is often used: thermal mass absorbs and stores heat, while insulation retains that heat within the building. Conductive materials, on the other hand, are generally avoided in thermal mass applications, as they allow heat to pass through quickly, undermining the effect of thermal inertia. - 2.4.2 Choosing Materials for Energy Efficiency
Selecting materials with appropriate thermal properties based on climate is essential for maximizing energy efficiency. In regions with hot days and cool nights, high thermal mass materials like stone and concrete can be highly effective, as they can absorb heat during the day and release it overnight. In contrast, in cooler climates where retaining heat is critical, thermal mass materials should be used with sufficient insulation to prevent rapid heat loss. Additionally, emerging materials such as PCMs can be integrated in strategic areas to optimize energy efficiency in all climates, offering adaptable solutions in sustainable building design. Reference: Gong, X., Akashi, Y., & Sumiyoshi, D. (2012). “Optimization of passive design measures.” Energy and Buildings, Elsevier.
- 2.4.1 Insulating vs. Conductive Materials
- 2.5 Thermal mass of common materials used in home construction
Below is a table listing the thermal mass properties of common building materials, along with their units for density and specific heat capacity, which together define thermal mass.
| Material | Density (kg/m³) | Specific Heat Capacity (J/kg·K) | Thermal Mass (J/m³·K) |
|---|---|---|---|
| Concrete | 2,400 | 880 | 2,112,000 |
| Brick | 1,800 | 840 | 1,512,000 |
| Stone (Granite) | 2,700 | 790 | 2,133,000 |
| Water | 1,000 | 4,180 | 4,180,000 |
| Gypsum Board (Drywall) | 800 | 1,090 | 872,000 |
| Wood (Softwood) | 500 | 2,300 | 1,150,000 |
| Insulating Concrete | 1,200 | 880 | 1,056,000 |
| Glass | 2,500 | 840 | 2,100,000 |
| Steel | 7,800 | 460 | 3,588,000 |
| Earth (Compacted) | 1,700 | 840 | 1,428,000 |
| Adobe | 1,600 | 920 | 1,472,000 |
| Plaster | 1,200 | 840 | 1,008,000 |
| Tile (Ceramic) | 2,200 | 840 | 1,848,000 |
| Sandstone | 2,400 | 710 | 1,704,000 |
| Fiberglass Insulation | 12 | 840 | 10,080 |
| Expanded Polystyrene (EPS) | 20 | 1,210 | 24,200 |
| Extruded Polystyrene (XPS) | 35 | 1,300 | 45,500 |
| Polyurethane Foam | 30 | 1,470 | 44,100 |
| Mineral Wool | 70 | 840 | 58,800 |
| Cellulose Insulation | 80 | 1,400 | 112,000 |
Notes:
- Thermal mass (J/m³·K) is calculated as:
![Rendered by QuickLaTeX.com \[\text{Thermal Mass} = \text{Density} \times \text{Specific Heat Capacity}\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-50761c95326ac9df158baa6cfda3e466_l3.png)
- Insulating materials like fiberglass, EPS, XPS, and mineral wool generally have low thermal mass compared to dense materials like concrete or brick but are effective at reducing heat transfer due to their low thermal conductivity. They help maintain interior temperatures by slowing heat flow rather than storing heat.
This table can be used to compare thermal storage and insulation characteristics when designing or retrofitting buildings with optimal thermal inertia and energy efficiency in mind.
3. Thermal Inertia and Its Relationship with Outdoor Temperature Fluctuations
Thermal inertia’s effectiveness in a building is significantly influenced by outdoor temperature changes. When temperatures fluctuate, particularly in climates with high day-to-night variability, buildings with adequate thermal mass can absorb and release heat slowly, stabilizing indoor temperatures and enhancing comfort. This section explores the role of thermal mass in temperature stabilization, the dynamics of heat transfer between indoor and outdoor environments, and the challenges associated with heat loss and thermal bridging.
- 3.1 The Role of Thermal Mass in Temperature Stabilization
- 3.1.1 Stabilizing Effect of High Thermal Mass
Buildings with high thermal mass are designed to resist rapid temperature changes by gradually absorbing and releasing heat. Materials with high thermal mass, such as concrete, brick, and stone, can absorb excess heat when outdoor temperatures rise, storing it until temperatures cool. As temperatures decrease, the stored heat is slowly released back into the indoor environment, preventing abrupt temperature drops inside the building. This buffering effect, known as “thermal lag,” reduces the need for heating or cooling, as the building naturally regulates its temperature. This stabilizing effect is most beneficial in climates where there is significant temperature variation between day and night. For example, in desert climates, where daytime temperatures are high and nights are significantly cooler, thermal mass helps maintain a comfortable indoor temperature without over-reliance on active HVAC systems. By slowing down the rate at which indoor temperatures respond to outdoor changes, thermal mass can improve occupant comfort and reduce energy costs, particularly in buildings with passive solar design elements. - 3.1.2 Benefits of Temperature Stabilization in Extreme Climates
In regions with extreme seasonal or daily temperature swings, the ability of thermal mass to stabilize indoor temperatures is crucial. In colder climates, high thermal mass materials absorb and retain warmth from sunlight during the day, releasing it gradually during colder evenings. This effect reduces the need for artificial heating, helping to keep energy consumption low and maintaining a comfortable environment. In hot climates, thermal mass can absorb indoor heat, reducing peak temperatures and providing a cooling effect at night when temperatures drop. Additionally, the stabilizing properties of thermal mass are valuable in urban areas where the heat island effect causes elevated temperatures. High thermal mass buildings in urban settings can help moderate indoor temperatures, reducing energy demand and contributing to urban sustainability goals by mitigating the impacts of urban heat. The use of thermal mass as a passive cooling and heating tool has become an important consideration in both residential and commercial building design, especially as energy efficiency becomes a higher priority. Reference: Cheng, V., & Ng, E. (2006). “Thermal inertia and its impact on urban climate.” Energy and Buildings, Elsevier.
- 3.1.1 Stabilizing Effect of High Thermal Mass
- 3.2 Heat Transfer Dynamics Between Indoor and Outdoor Environments
- 3.2.1 Indoor-Outdoor Temperature Gradient
The temperature difference, or gradient, between indoor and outdoor environments plays a key role in heat transfer dynamics and the effectiveness of thermal inertia. When there is a large temperature difference, heat will naturally flow from the warmer area to the cooler area. Thermal inertia in high thermal mass materials moderates this heat flow by absorbing or releasing heat based on the gradient. During hot days, high thermal mass materials absorb some of the outdoor heat that tries to penetrate the building, keeping indoor temperatures lower. Conversely, in cold weather, they retain indoor warmth, slowing the rate at which it escapes. This temperature gradient effect is central to designing buildings for passive climate control. By managing heat transfer across the building envelope, thermal inertia reduces the load on HVAC systems and enhances indoor comfort. For example, a well-insulated building with high thermal mass can maintain an internal temperature closer to the daily average temperature, as opposed to mirroring outdoor fluctuations. This results in lower peak heating and cooling demands, optimizing energy efficiency. - 3.2.2 Thermal Bridging and Heat Loss
While thermal mass can moderate heat transfer, certain construction features can bypass or “bridge” this effect, leading to energy loss. Thermal bridges are areas in a building where heat can flow more easily, often through conductive materials or poorly insulated joints between structural elements. Common examples include metal window frames, poorly insulated corners, or gaps in wall insulation. These points allow heat to bypass high thermal mass materials, undermining the building’s overall thermal performance. Minimizing thermal bridging is essential to harness the full benefits of thermal inertia. Building design strategies to reduce thermal bridging include continuous insulation, careful detailing of window and door frames, and using materials with low thermal conductivity in key areas. By addressing these potential weak points, designers can maximize the building’s capacity for temperature stabilization, allowing the thermal mass to perform its role in maintaining a steady indoor climate. Additionally, advanced techniques, such as using insulated metal panels or thermal breaks, can be integrated to reduce the impact of thermal bridges, further enhancing the building’s energy efficiency. Reference: Lomas, K. J., & Eppel, H. (1992). “Thermal response of buildings.” Building and Environment, Elsevier.
- 3.2.1 Indoor-Outdoor Temperature Gradient
4. Thermal Inertia’s Role in Seasonal Climate Adaptation
Thermal inertia’s ability to store and gradually release heat makes it an invaluable asset in adapting buildings to seasonal climate variations. In winter, thermal mass helps retain indoor warmth, reducing heating needs, while in summer, it mitigates heat gain, thereby lowering cooling demands. By understanding and optimizing thermal inertia, buildings can maintain comfortable indoor conditions year-round, cutting down on energy consumption and fostering sustainable design.
- 4.1 Thermal Inertia and Winter Heating Demand
- 4.1.1 Retaining Heat in Cold Climates
In winter, thermal mass materials within a building absorb heat from the sun during daylight hours, even when temperatures are low. This stored heat is slowly released as temperatures drop in the evening and at night, helping to maintain a warmer indoor environment. High thermal inertia materials like stone, concrete, or adobe are especially useful in cold climates because they retain this heat over extended periods, reducing the need for continuous heating. By delaying heat loss, thermal mass stabilizes indoor temperatures, providing a buffer against cold outdoor air. This characteristic is particularly beneficial in passive solar design, where south-facing windows allow sunlight to enter and warm the thermal mass in floors and walls. During the night, the stored heat radiates back into the space, minimizing the temperature drop indoors. This process allows buildings to retain warmth more effectively, ensuring comfort without heavy reliance on heating systems. - 4.1.2 Energy Savings in Winter with Thermal Mass
Effective use of thermal mass in winter can significantly lower energy consumption. By reducing the frequency and intensity of heating, thermal mass enables energy savings, which translates to lower heating costs and a smaller environmental footprint. For example, a well-designed passive solar building with sufficient thermal mass may require less energy input to maintain a stable indoor temperature, as the thermal mass absorbs, stores, and redistributes solar heat. Studies indicate that incorporating thermal inertia into building design can reduce winter heating demands by up to 30% in some climates, underscoring the energy efficiency benefits of thermal mass. Reference: Santamouris, M. (2019). Cooling Energy Solutions for Buildings and Cities. Elsevier.
- 4.1.1 Retaining Heat in Cold Climates
- 4.2 Thermal Inertia and Summer Cooling Demand
- 4.2.1 Passive Cooling in Hot Seasons
In summer, thermal mass plays an essential role in passive cooling by absorbing indoor heat during the day and releasing it when temperatures drop in the evening. Buildings with high thermal mass can buffer against the midday heat, keeping indoor temperatures cooler even without active air conditioning. For example, thick concrete or stone walls absorb excess heat and prevent it from immediately impacting indoor spaces. This delay in heat transfer, known as thermal lag, allows indoor temperatures to remain stable during peak outdoor temperatures, making indoor spaces more comfortable. Passive cooling through thermal inertia is particularly advantageous in climates with hot days and cool nights, such as arid or Mediterranean regions. In such climates, buildings with high thermal mass stay cool during the day and release the stored heat at night, naturally regulating indoor temperature. As a result, occupants benefit from a more comfortable environment with less need for mechanical cooling, which can contribute to significant energy savings over the summer months. - 4.2.2 Lowering Cooling Loads
By moderating indoor temperatures, thermal inertia helps reduce the cooling load on HVAC systems. High thermal mass buildings absorb solar radiation and internal heat gains, slowing the rate at which indoor temperatures rise. Consequently, air conditioning systems do not need to work as hard to maintain a comfortable environment, leading to lower energy consumption and operating costs. Additionally, thermal mass can work in tandem with other passive cooling strategies, such as natural ventilation and shading, to further reduce cooling demands. In some cases, thermal inertia can lead to a reduction in peak cooling loads by up to 40%, especially when combined with proper building orientation and shading devices. Reference: Kolokotroni, M., & Aronis, A. (1999). “The influence of the London urban heat island on building summer cooling demand.” Solar Energy, Elsevier.
- 4.2.1 Passive Cooling in Hot Seasons
- 4.3 Optimizing Seasonal Comfort through Building Design
- 4.3.1 Designing for Thermal Inertia by Climate
The effectiveness of thermal inertia varies based on the local climate, making it essential to tailor building design accordingly. In regions with hot summers and cold winters, buildings should incorporate both thermal mass and insulation to maximize seasonal comfort. For instance, in colder climates, maximizing sun exposure to thermal mass materials during the winter can help capture and store heat, while in hot climates, minimizing direct solar exposure to thermal mass can prevent overheating. Additionally, building orientation, window placement, and the use of shading devices must be considered to optimize thermal inertia benefits throughout the year. Buildings in regions with milder climates can also benefit from thermal inertia, though the design considerations may differ. In temperate zones, where seasonal temperature swings are less extreme, moderate amounts of thermal mass can help maintain comfort without requiring intensive heating or cooling. For designers, understanding the unique climate characteristics of the building site enables more effective utilization of thermal inertia for both energy savings and occupant comfort. - 4.3.2 Material Choice and Seasonal Adaptability
Selecting materials suited for both winter heat retention and summer cooling is crucial to leveraging thermal inertia effectively. Dense materials like concrete, brick, and stone are typically chosen for their high thermal capacity, but newer materials, such as phase change materials (PCMs), can adapt to seasonal changes even more efficiently. PCMs, for example, can absorb and release heat at specific temperatures, providing a more tailored approach to seasonal climate adaptation. They can enhance thermal inertia by storing and releasing heat in response to temperature changes, offering a dynamic way to balance heating and cooling demands throughout the year. Furthermore, the placement of these materials within the building is essential. For optimal effectiveness, thermal mass should be positioned in areas where it can receive direct sunlight in winter and be shaded in summer. By integrating shading solutions, such as overhangs, blinds, or vegetation, buildings can manage solar gains more effectively, allowing thermal mass to support seasonal climate adaptation and providing a high level of indoor comfort regardless of external temperatures. Reference: Givoni, B. (1994). Passive and Low Energy Cooling of Buildings. John Wiley & Sons.
- 4.3.1 Designing for Thermal Inertia by Climate
5. The Role of Windows and Insulation in Modulating Thermal Inertia
Windows and insulation are key elements in regulating a building’s thermal inertia. Insulation can either enhance or limit the effects of thermal mass, while windows and glazing impact heat exchange by allowing or blocking solar radiation. Together, these components play a critical role in achieving optimal temperature control, enhancing energy efficiency, and maximizing the benefits of thermal inertia.
- 5.1 Insulation: Enhancing or Limiting Thermal Inertia
- 5.1.1 Insulation Materials and Thermal Mass
Insulation and thermal mass have complementary roles in building design. Thermal mass absorbs, stores, and releases heat, helping to stabilize indoor temperatures, while insulation slows the rate at which heat enters or leaves the building. The effectiveness of thermal inertia depends not only on the thermal mass within a building but also on how well it is insulated. Insulation materials, such as fiberglass, foam, and cellulose, provide a thermal barrier, reducing heat transfer through walls, ceilings, and floors. Different insulation materials offer varying levels of thermal resistance (R-value), which measures their ability to limit heat flow. High-R-value materials, like spray foam, are often used in regions with extreme climates to enhance the building’s thermal performance. However, while insulation restricts unwanted heat transfer, it also affects the efficiency of thermal mass by reducing its ability to absorb and release heat effectively. Thus, the balance between thermal mass and insulation must be carefully considered to optimize the building’s thermal response to seasonal and daily temperature changes. - 5.1.2 Balancing Insulation and Thermal Mass for Optimal Efficiency
Achieving a balance between insulation and thermal mass is essential for energy-efficient building design. In climates with high temperature fluctuations, using both thermal mass and insulation effectively can significantly reduce heating and cooling loads. For instance, in winter, insulation prevents heat loss, allowing the thermal mass to retain indoor warmth for longer periods. In summer, insulation restricts heat gain from outside, helping the thermal mass maintain cooler indoor temperatures. To maximize this balance, designers often place insulation on the exterior of thermal mass materials, such as in insulated concrete forms (ICFs), which combine insulation with thermal mass in a single unit. This configuration allows the thermal mass to interact with the interior environment while preventing heat loss or gain from the exterior. Additionally, strategic insulation placement, such as double-wall construction or insulated roofing, can further enhance thermal inertia by controlling how much heat enters or leaves the building. When properly balanced, insulation and thermal mass create a synergy that enhances comfort and reduces energy consumption throughout the year. Reference: Gong, X., Akashi, Y., & Sumiyoshi, D. (2012). “Optimization of passive design measures.” Energy and Buildings, Elsevier.
- 5.1.1 Insulation Materials and Thermal Mass
- 5.2 Glazing and Thermal Exchange in Homes
- 5.2.1 Window Placement and Solar Heat Gain
Windows play a pivotal role in regulating a building’s internal temperature by allowing sunlight to enter and contribute to heat gain. The positioning and size of windows are crucial in managing thermal inertia, as they determine how much solar radiation reaches the building’s thermal mass. South-facing windows, for instance, maximize sunlight exposure during winter in the Northern Hemisphere, providing a natural source of heat. In contrast, in hot climates, strategically placed windows with limited direct sunlight exposure can minimize solar heat gain, keeping indoor spaces cooler. Properly positioned windows allow thermal mass to absorb and store solar heat during the day, releasing it gradually as indoor temperatures drop. By controlling the amount of sunlight that enters the building, window placement influences the effectiveness of thermal mass and contributes to passive heating and cooling. For maximum benefit, building designs often include overhangs, awnings, or louvers above south-facing windows to block summer sun while allowing winter sunlight to enter, balancing the seasonal impact on thermal inertia. - 5.2.2 Glazing Techniques to Enhance Thermal Control
Advanced glazing techniques can further optimize thermal inertia by improving insulation and regulating solar heat gain. Double glazing, for example, consists of two panes of glass with a sealed air or gas-filled gap between them, which reduces heat transfer and enhances insulation. This technique minimizes heat loss in winter and restricts heat gain in summer, complementing the building’s thermal mass. Triple glazing and low-emissivity (low-E) coatings offer additional insulation and reflect infrared heat, providing a more controlled indoor environment. In buildings with high thermal mass, glazing techniques that reduce excessive heat gain or loss allow the thermal mass to function effectively, keeping interior temperatures stable. Low-E coatings, for instance, selectively reflect solar radiation while allowing visible light to pass through, reducing unwanted heat in summer while retaining warmth in winter. By carefully selecting and positioning windows with the appropriate glazing, building designers can maximize the benefits of thermal inertia and improve overall energy efficiency. Reference: Givoni, B. (1994). Passive and Low Energy Cooling of Buildings. John Wiley & Sons.
- 5.2.1 Window Placement and Solar Heat Gain
- 5.3 Modulating Thermal Inertia with Shades and Curtains
- 5.3.1 Using Shades to Control Solar Heat Gain
- 5.3.1.1 Reflective and Insulating Shades
Reflective and insulating shades are effective tools for managing solar heat gain and supporting thermal inertia. Reflective shades can block a significant amount of solar radiation, reducing heat gain during the summer months. Insulating shades, on the other hand, help retain heat in winter by providing an additional layer of insulation at night, preventing heat loss through windows. These types of shades allow for seasonal adaptability, enhancing comfort and reducing HVAC demand. - 5.3.1.2 Automatic Shades and Smart Control Integration
Automatic shades and smart shading systems offer enhanced control by adjusting their position based on real-time data such as temperature, sunlight intensity, and time of day. These systems can be programmed to open in the morning to allow sunlight in during colder months and to close in the afternoon to block intense sunlight in warmer months. This dynamic approach maximizes the benefits of thermal inertia by regulating solar heat gain and reducing HVAC needs, making it a valuable addition to energy-efficient building design. Reference: Wang, Z., & Zhang, X. (2017). “Shading strategies and control technologies for energy-efficient buildings.” Renewable and Sustainable Energy Reviews, Elsevier.
- 5.3.1.1 Reflective and Insulating Shades
- 5.3.2 Using Curtains to Enhance Thermal Buffering
- 5.3.2.1 Heavy Curtains for Nighttime Insulation
Heavy curtains act as thermal barriers, particularly useful in colder climates. When drawn at night, thick curtains reduce heat loss through windows by creating a layer of insulation that slows down heat transfer. By preventing heat from escaping, these curtains help maintain warmer indoor temperatures, complementing the thermal mass of the building by reducing the load on heating systems. - 5.3.2.2 Light Curtains for Daytime Heat Management
Light, sheer curtains can help manage heat during the day by filtering sunlight, preventing excessive solar heat gain, and diffusing natural light. They allow for controlled daylight entry without significantly heating the indoor space, making them effective in maintaining a balanced indoor environment in summer. Light curtains help reduce the need for active cooling, working alongside thermal mass to keep indoor temperatures comfortable. - 5.3.2.3 Layered Curtain Systems for Adaptable Thermal Control
Layered curtain systems offer versatility in thermal control by allowing users to adapt to different times of day and seasons. For example, a layered system could include a heavy inner curtain for winter insulation and a lighter outer curtain for summer shading. By adjusting curtain layers as needed, occupants can enhance the building’s thermal inertia, improving comfort and efficiency. Layered curtains are particularly useful in regions with pronounced seasonal changes, where they can provide both insulation and shading to support passive heating and cooling strategies. Reference: Givoni, B. (1994). Passive and Low Energy Cooling of Buildings. John Wiley & Sons.
- 5.3.2.1 Heavy Curtains for Nighttime Insulation
- 5.3.1 Using Shades to Control Solar Heat Gain
6. Thermal Lag and Thermal Inertia: How It Works in Homes
Thermal lag is a fundamental concept related to thermal inertia, referring to the time delay between a change in temperature outside and its impact on indoor temperature. This delay occurs because thermal mass within a building absorbs heat slowly and releases it gradually, creating a buffer against rapid temperature swings. Thermal lag is especially beneficial in passive climate control, where it helps regulate indoor temperatures naturally, reducing reliance on active heating and cooling systems. This section explains thermal lag, its benefits, and how it can be optimized through design and automation.
- 6.1 Definition of Thermal Lag and Its Benefits
- 6.1.1 Understanding Thermal Lag
Thermal lag describes the time delay between temperature changes in a building’s exterior environment and the corresponding impact on its indoor temperature. This phenomenon occurs because materials with high thermal mass, such as concrete, brick, and stone, absorb and release heat slowly. When outdoor temperatures fluctuate, thermal mass materials gradually respond, storing heat during warmer periods and releasing it during cooler periods. This delayed response, or “thermal lag,” acts as a natural buffer against sudden temperature changes, maintaining more stable indoor conditions. For example, if temperatures peak in the afternoon, a building with high thermal mass might only experience the temperature increase several hours later. This delay in temperature transmission is particularly useful in climates with large daily temperature variations, such as deserts, where days are hot, and nights are cool. By buffering against these fluctuations, thermal lag contributes to a more comfortable indoor environment. - 6.1.2 Advantages of Thermal Lag in Temperature Stabilization
Thermal lag enhances comfort by preventing rapid temperature changes indoors. This stabilization effect means that occupants experience more consistent temperatures, even as outdoor conditions shift throughout the day. For instance, in a building with high thermal mass, indoor temperatures remain relatively stable during hot afternoons, as the walls absorb heat without immediately transferring it indoors. As outdoor temperatures cool in the evening, the stored heat is then gradually released, creating a warming effect. The benefits of thermal lag extend to energy savings as well. By reducing the frequency and intensity of heating and cooling cycles, buildings with high thermal lag experience reduced HVAC loads, which translates into lower energy costs. Additionally, thermal lag minimizes peak energy demand, which is beneficial for grid stability and can lead to further cost savings in regions with time-of-use pricing. Reference: Hoes, P., & Trčka, M. (2011). “Energy and thermal comfort performance of buildings: The role of building thermal mass.” Energy and Buildings, Elsevier.
- 6.1.1 Understanding Thermal Lag
- 6.2 Thermal Lag and Time-Delayed Temperature Adjustments
- 6.2.1 Role of Thermal Lag in Passive Heating
Thermal lag plays an important role in passive heating strategies, particularly in colder climates. During the day, sunlight enters a building and is absorbed by materials with high thermal mass. These materials retain the heat and then release it slowly as temperatures drop in the evening. This effect can maintain warmth throughout the night, reducing the need for additional heating. Passive solar buildings are often designed with thermal mass positioned to capture sunlight during the day, maximizing the effectiveness of thermal lag in keeping indoor spaces warm after the sun sets. For example, a concrete floor exposed to direct sunlight will absorb solar energy throughout the day and release it during the evening hours. This “free” heating effect is a cornerstone of passive solar design, where the goal is to maintain comfortable indoor temperatures without active heating systems. By timing the heat release to coincide with cooler night temperatures, thermal lag helps sustain warmth and conserves energy. - 6.2.2 Cooling Delay Through Thermal Lag
In hot climates, thermal lag can be leveraged to delay the impact of peak daytime temperatures until later in the day. Buildings with significant thermal mass absorb heat gradually, preventing the indoor temperature from rising too quickly. This delayed response allows occupants to benefit from cooler indoor temperatures during the hottest part of the day. In the evening, when outdoor temperatures drop, ventilation can be used to dissipate the stored heat, preparing the building for another day of solar exposure. For instance, in a thick adobe or concrete-walled home, the walls will absorb heat during the day without immediately increasing indoor temperatures. As the day progresses, the indoor temperature rise is minimal, allowing occupants to enjoy cooler interiors. Later in the evening, if needed, the building can release the stored heat into the cooler night air, enhancing comfort without active cooling. Reference: Santamouris, M. (2019). Cooling Energy Solutions for Buildings and Cities. Elsevier.
- 6.2.1 Role of Thermal Lag in Passive Heating
- 6.3 Applications of Thermal Lag in Passive Climate Control
- 6.3.1 Designing with Thermal Lag in Mind
To effectively leverage thermal lag, building designs should consider the orientation, placement, and type of thermal mass materials. For example, in passive solar homes, materials with high thermal mass are strategically placed in areas that receive direct sunlight, such as south-facing walls or floors. By designing to maximize sun exposure in winter and minimize it in summer, thermal lag can be harnessed to provide seasonal comfort. Other design elements, such as window placement, shading devices, and ventilation strategies, also play a role. Shading can prevent excessive heat gain in summer, reducing the demand on cooling systems, while allowing sunlight to warm thermal mass in winter. Additionally, natural ventilation can enhance the effectiveness of thermal lag by dissipating stored heat when necessary, especially in climates with significant nighttime cooling. - 6.3.2 Thermal Lag as a Complement to Insulation
While thermal lag stabilizes temperatures, insulation further enhances this effect by slowing down heat transfer through walls and roofs. When combined, thermal mass and insulation work to create a more comfortable and efficient indoor environment. For example, in cold weather, insulated thermal mass holds heat longer, releasing it slowly over time, which can reduce heating needs. In warm climates, insulated thermal mass absorbs heat during the day without transferring it indoors, while insulation prevents external heat from entering. Buildings with both thermal mass and high insulation achieve optimal thermal performance, as the insulation prevents rapid heat loss or gain, allowing the thermal mass to maintain a consistent indoor temperature. By complementing thermal lag with insulation, buildings can improve comfort and energy efficiency, regardless of the external climate. Reference: Givoni, B. (1994). Passive and Low Energy Cooling of Buildings. John Wiley & Sons.
- 6.3.1 Designing with Thermal Lag in Mind
- 6.4 Automation with Thermal Lag Prediction Algorithms
Thermal lag prediction algorithms play an essential role in modern home automation by enabling heating, ventilation, and air conditioning (HVAC) systems to anticipate temperature needs based on the thermal properties of building materials. By understanding how long it takes for temperature changes to penetrate through the building envelope, these algorithms enable smart systems to manage energy more efficiently and maintain indoor comfort with minimal HVAC intervention. Here, we explore specific algorithms and explain their mechanisms and applications in leveraging thermal lag for passive heating and cooling.
- 6.4.1 Time-Delayed Heating and Cooling Calculations Time-delayed heating and cooling algorithms are designed to predict when the HVAC system should begin operating, based on the thermal lag characteristics of the building materials. These algorithms factor in external temperature forecasts, building orientation, thermal mass, insulation levels, and desired indoor temperatures. Two common approaches to implementing time-delayed HVAC control include: Algorithm 1: Simple Predictive Time-Delay (PTD) Algorithm
The PTD algorithm estimates the time required for a temperature change outside to impact the indoor environment. It applies a fixed delay based on the thermal properties of the building’s materials and the current rate of outdoor temperature change. Here’s how the PTD algorithm can be structured:- Input Parameters:
- Outdoor temperature (
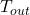 ): Forecasted outdoor temperature for the next few hours.Thermal mass coefficient (
): Forecasted outdoor temperature for the next few hours.Thermal mass coefficient (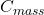 ): Characteristic of building materials, indicating how quickly they absorb and release heat.Desired indoor temperature (
): Characteristic of building materials, indicating how quickly they absorb and release heat.Desired indoor temperature (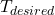 ): Preferred indoor temperature set by occupants.
): Preferred indoor temperature set by occupants.
Calculate the time delay (Δt) based on the rate of outdoor temperature change and the thermal mass coefficient:![Rendered by QuickLaTeX.com \[\Delta t = \frac{C_{mass}}{\Delta T_{out}/\Delta t}\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-5539f667c0067faac2c22c659e09f6b2_l3.png)
where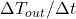 is the rate of change of outdoor temperature.HVAC Activation:
is the rate of change of outdoor temperature.HVAC Activation:
Schedule the HVAC system to start or stop Δt hours before the indoor temperature is expected to reach the threshold. If heating is required, the HVAC is scheduled to start early if temperatures are expected to drop sharply outside. Conversely, cooling is initiated if external temperatures are forecasted to rise, but with a delay calculated by Δt.Adaptive Adjustment:
As outdoor temperature changes throughout the day, the algorithm recalculates Δt and adjusts the HVAC start/stop time to maintain consistent comfort. Algorithm 2: Thermal Mass Adjusted Time-Delay (TMATD) Algorithm
The TMATD algorithm extends the basic PTD approach by factoring in additional variables such as internal heat gains (e.g., from appliances) and variations in building insulation levels. This approach is useful for homes with mixed materials (e.g., concrete and wood) that exhibit different thermal properties. - Outdoor temperature (
- Step 1: Determine the effective thermal mass coefficient, accounting for insulation and thermal mass material distribution.
- Step 2: Use a weighted average to calculate the effective thermal delay (Δt_effective) for different zones in the building:
![Rendered by QuickLaTeX.com \[\Delta t_{effective} = \frac{\sum (C_{mass,i} \times A_{i})}{\sum A_{i}}\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-e83933ab7bde5ee07a003ff881029023_l3.png)
where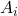 is the area of each material exposed to outdoor conditions.
is the area of each material exposed to outdoor conditions. - Step 3: Adjust the HVAC schedule by Δt_effective and update dynamically as outdoor temperatures change. Detailed Explanation: The PTD and TMATD algorithms enable HVAC systems to adapt in real-time by anticipating the impact of outdoor temperature changes based on the specific thermal properties of the home. By incorporating both the thermal mass and insulation levels, these algorithms improve energy efficiency and help maintain a stable indoor environment.
- Input Parameters:
- 6.4.2 Predictive Thermal Control for Passive Cooling Predictive thermal control algorithms go beyond simple time-delay algorithms by incorporating machine learning models and weather forecast data to predict temperature trends and adjust HVAC settings accordingly. Two common predictive thermal control algorithms are explained below: Algorithm 3: Model Predictive Control (MPC) with Thermal Lag Consideration
Model Predictive Control (MPC) is an advanced approach that uses a mathematical model of the building’s thermal properties to predict future indoor temperatures based on external conditions. Here’s how an MPC algorithm with thermal lag considerations might work:- Define a Thermal Model of the Building:
- Thermal mass model: The thermal properties of the building’s structure (e.g., walls, floors) are used to simulate the heat absorption and release dynamics.
- Energy balance equations: Energy flow in and out of the building is modeled based on internal gains, external temperature, and HVAC input.
- Input Variables:
- Weather forecast: Projected outdoor temperature, solar radiation, and humidity over the next 24 hours.
- Thermal mass properties: Material-specific heat capacity and thermal conductivity.
- HVAC control settings: Desired indoor temperature range and system constraints.
- Optimization and Prediction:
The algorithm uses predictive calculations to determine the optimal HVAC settings over a rolling time horizon (e.g., 24 hours) to maintain indoor temperature stability with minimal energy usage. The system forecasts indoor temperatures, considering thermal lag, and adjusts HVAC operation accordingly. - Continuous Feedback Loop:
The MPC algorithm updates predictions at each time step based on actual indoor and outdoor conditions, refining the HVAC response for improved efficiency. Explanation: MPC is particularly effective for homes with significant thermal mass, as it enables HVAC systems to anticipate temperature trends and make gradual adjustments. By predicting and adapting to thermal lag, MPC reduces the need for frequent temperature corrections, thereby lowering energy consumption. Algorithm 4: Reinforcement Learning (RL) Based Thermal Management
Reinforcement Learning (RL) is a machine learning technique where the HVAC system learns to optimize temperature control over time through a trial-and-error approach. An RL model can be designed to manage thermal lag by learning the relationship between outdoor temperatures, thermal mass properties, and indoor comfort needs.
- State Variables:
The RL agent considers variables such as current indoor temperature, outdoor temperature, rate of temperature change, and HVAC state (on/off). - Reward Function:
The reward function encourages actions that minimize energy use while maintaining indoor comfort. For example, the agent receives positive rewards for keeping the temperature within the desired range without excessive HVAC use, penalizing overuse of energy. - Action and Decision Process:
The RL agent chooses HVAC actions (heating, cooling, or idle) based on its learned understanding of how thermal lag will impact indoor temperature. The system continuously learns from real-time data, improving its response to temperature fluctuations over time. - Learning and Adaptation:
The RL model uses a dynamic feedback loop to adapt its decisions as it encounters new temperature scenarios. Over time, it learns optimal start/stop times based on thermal lag characteristics, weather patterns, and indoor comfort preferences. Detailed Explanation: RL-based predictive control is particularly suited for complex buildings with multiple zones and mixed-material thermal mass. By “learning” thermal lag patterns over time, RL algorithms become highly effective at minimizing energy consumption without compromising comfort. This model is beneficial for smart homes equipped with sensors, as it continuously adjusts based on real-world data, offering a self-optimizing solution for HVAC control.
- Define a Thermal Model of the Building:
7. Thermal Inertia and Energy Efficiency in Home Climate Control
Thermal inertia—the ability of materials to absorb and release heat gradually—has significant potential for enhancing energy efficiency in home climate control. By naturally moderating indoor temperatures, thermal inertia reduces dependency on active heating and cooling systems, lowers energy costs, and supports sustainable environmental practices. This section explores how thermal inertia leads to reduced HVAC usage, lower peak energy demand, and decreased carbon emissions, as well as specific algorithms that optimize HVAC schedules by leveraging thermal inertia data.
- 7.1 Energy Savings through Reduced HVAC Usage
- 7.1.1 Minimizing Heating and Cooling Loads
Thermal inertia reduces the need for constant heating and cooling adjustments by naturally stabilizing indoor temperatures. High thermal mass materials, such as concrete and brick, absorb excess heat during warm periods and release it slowly when temperatures drop. This natural temperature regulation decreases reliance on HVAC systems, especially in climates with significant temperature fluctuations. Studies suggest that homes with high thermal mass require 20-30% less heating and cooling energy than those with low thermal mass due to their ability to buffer temperature changes passively (Santamouris & Kolokotsa, 2013). For instance, in a region with substantial day-to-night temperature swings, a home built with high thermal mass materials will stay cooler during the day, reducing the need for air conditioning. At night, as temperatures drop, the thermal mass releases stored heat, diminishing the need for heating. This process reduces the load on HVAC systems, translating into substantial energy savings. - 7.1.2 Lower Energy Bills through Efficient Climate Control
By reducing the active demand on HVAC systems, thermal inertia directly contributes to lower energy bills. Reductions in heating and cooling costs are especially notable in regions with extreme seasonal temperatures, where HVAC demand is high. Research by Santamouris and Kolokotsa demonstrates that homes with enhanced thermal inertia can achieve energy cost reductions of up to 15-25% due to decreased HVAC runtime (Santamouris & Kolokotsa, 2013, Energy and Buildings, Elsevier). Additionally, reduced HVAC operation contributes to lower maintenance costs and extends the equipment’s lifespan, delivering long-term cost savings.
- 7.1.1 Minimizing Heating and Cooling Loads
- 7.2 Thermal Inertia’s Contribution to Lower Energy Bills
- 7.2.1 The Role of Passive Heating and Cooling
Thermal inertia supports passive heating and cooling, an essential aspect of energy-efficient building design. By storing heat during warm hours and releasing it during cooler periods, thermal mass reduces the need for artificial heating and cooling. A study on passive solar heating shows that using thermal mass materials, in combination with passive solar designs, can reduce heating costs by up to 30% in colder climates (Santamouris, 2019, Cooling Energy Solutions for Buildings and Cities, Elsevier). In hot climates, the same principle applies to cooling. Buildings with high thermal mass can remain cooler during peak heat hours, allowing for passive cooling. Additional ventilation at night to release stored heat further amplifies this effect, reducing daytime energy demand and creating a more comfortable indoor environment without relying on active cooling systems. - 7.2.2 Reducing Peak Energy Demand
Peak energy demand often occurs during the hottest and coldest times of the day, significantly impacting energy costs and grid stability. Buildings with high thermal inertia delay indoor temperature changes relative to outdoor fluctuations, which helps avoid immediate peak-hour energy needs. For instance, while outdoor temperatures may peak in the afternoon, a high thermal mass building will only gradually increase in temperature, reducing immediate cooling needs. Reducing peak energy demand has economic and environmental benefits. Research suggests that reducing peak load through thermal inertia can save up to 10-20% in energy costs, especially in regions with high temperature variability (Santamouris, 2019). Additionally, balancing demand during peak times alleviates stress on the power grid, providing a stable energy supply and reducing the need for high-emission peak energy sources.
- 7.2.1 The Role of Passive Heating and Cooling
- 7.3 Environmental Benefits of Reduced Energy Demand
- 7.3.1 Carbon Footprint Reduction
By lowering HVAC demands, thermal inertia reduces greenhouse gas emissions. HVAC systems are substantial contributors to carbon emissions, often powered by fossil fuels or energy-intensive processes. Reducing HVAC energy requirements by even 10% can lead to significant reductions in CO₂ emissions, especially when scaled across residential buildings. Studies indicate that effective use of thermal mass can reduce a building’s carbon footprint by up to 20% compared to traditional low-mass buildings (Lomas & Eppel, 1992, Building and Environment, Elsevier). By utilizing thermal inertia, homeowners contribute to global carbon reduction efforts. Additionally, reducing HVAC usage during peak times decreases reliance on non-renewable energy sources, aligning with sustainability goals and lessening the environmental impact of home energy consumption. - 7.3.2 Energy Efficiency and Sustainable Building Design
Thermal inertia is integral to sustainable building design, with many green building certifications (e.g., LEED) emphasizing energy efficiency. Using materials with high thermal mass is a recognized strategy for achieving energy efficiency benchmarks, as it enhances energy performance and reduces environmental impact. Thermal inertia also supports net-zero energy building goals, where buildings produce as much energy as they consume by lowering the overall energy demand. This synergy between passive thermal regulation and renewable energy use promotes resilient and sustainable building practices.
- 7.3.1 Carbon Footprint Reduction
- 7.4 HVAC Scheduling Optimization Algorithm Using Thermal Inertia
- 7.4.1 Load Balancing Algorithm for Energy Peaks
The Load Balancing Algorithm for Energy Peaks uses thermal inertia to balance HVAC loads and prevent high energy demand during peak times. This algorithm schedules HVAC usage to leverage thermal mass, ensuring energy consumption is minimized during peak hours by pre-conditioning the indoor environment in advance. Algorithm: Thermal Pre-conditioning for Peak Load Reduction- Input Parameters:Thermal Mass (
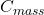 ): Quantifies the building’s heat storage capacity.Outdoor Temperature Forecast (T
): Quantifies the building’s heat storage capacity.Outdoor Temperature Forecast (T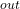 ): Predicted outdoor temperatures over the next 12-24 hours.Indoor Temperature Set Point (
): Predicted outdoor temperatures over the next 12-24 hours.Indoor Temperature Set Point (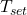 ): Desired indoor temperature range.Energy Pricing Schedule: Time-of-use pricing data indicating peak and off-peak times.Prediction of Thermal Response:Calculate the building’s thermal lag, the delay in indoor temperature change relative to outdoor changes, using:
): Desired indoor temperature range.Energy Pricing Schedule: Time-of-use pricing data indicating peak and off-peak times.Prediction of Thermal Response:Calculate the building’s thermal lag, the delay in indoor temperature change relative to outdoor changes, using:![Rendered by QuickLaTeX.com \[\Delta t = \frac{C_{mass}}{k \times \Delta T_{out}}\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-1fbda85a71556008d363efdd78543aeb_l3.png)
where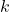 is a constant based on material conductivity and area, and
is a constant based on material conductivity and area, and 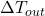 is the anticipated outdoor temperature change.Pre-conditioning Schedule Calculation:Schedule HVAC pre-conditioning based on thermal lag. For instance:
is the anticipated outdoor temperature change.Pre-conditioning Schedule Calculation:Schedule HVAC pre-conditioning based on thermal lag. For instance:![Rendered by QuickLaTeX.com \[t_{pre-cool} = T_{peak} - \Delta t\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-98b397ea6c942ef5569e53f4c5b4881a_l3.png)
Pre-conditioning starts at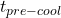 to ensure indoor comfort by the peak period.Real-time Adjustment:Continuously monitor indoor and outdoor conditions to adjust HVAC schedules if conditions change unexpectedly.
to ensure indoor comfort by the peak period.Real-time Adjustment:Continuously monitor indoor and outdoor conditions to adjust HVAC schedules if conditions change unexpectedly.
- Input Parameters:Thermal Mass (
- 7.4.2 Optimizing Power Usage Using Thermal Inertia Data
This algorithm leverages time-of-use (TOU) energy pricing to minimize HVAC costs, primarily using low-cost hours to condition the building’s thermal mass. Integrating real-time data on thermal mass and energy pricing, this strategy aligns HVAC operation with economic efficiency. Algorithm: Time-of-Use (TOU) Based HVAC Optimization- Input Parameters:Thermal Mass Coefficient (
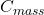 ): Represents the heat storage capability of building materials.Energy Cost Data (
): Represents the heat storage capability of building materials.Energy Cost Data (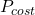 ): Hourly pricing information.Temperature Forecasts: Indoor and outdoor temperature predictions.Occupancy Schedule (
): Hourly pricing information.Temperature Forecasts: Indoor and outdoor temperature predictions.Occupancy Schedule (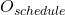 ): Expected occupancy for preferred comfort times.Thermal Simulation and Cost Prediction:Simulate the temperature response based on thermal inertia and HVAC schedules to estimate power consumption:
): Expected occupancy for preferred comfort times.Thermal Simulation and Cost Prediction:Simulate the temperature response based on thermal inertia and HVAC schedules to estimate power consumption:
Minimize total energy costs over 24 hours by setting:![Rendered by QuickLaTeX.com \[E_{HVAC}(t) = P_{HVAC} \times \Delta t\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-6a3e5b9d1e72f73d8f572a734ac27b84_l3.png)
Scheduling HVAC for Off-Peak Pricing:During off-peak periods, the algorithm “charges” the building’s thermal mass by cooling or heating within the comfort range, reducing active HVAC use during peak periods.Real-Time Adaptive Control:Continuously adapt to changes in outdoor temperatures or energy prices by re-evaluating HVAC scheduling to optimize both comfort and cost.![Rendered by QuickLaTeX.com \[\text{Minimize } \sum (E_{HVAC}(t) \times P_{cost}(t))\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-b15e11ddb8557622d188cece2114a3d6_l3.png)
- Input Parameters:Thermal Mass Coefficient (
- 7.4.1 Load Balancing Algorithm for Energy Peaks
References:
- Santamouris, M., & Kolokotsa, D. (2013). “Passive cooling dissipation techniques.” Energy and Buildings, Elsevier.
- Santamouris, M. (2019). Cooling Energy Solutions for Buildings and Cities. Elsevier.
- Lomas, K. J., & Eppel, H. (1992). “Thermal response of buildings.” Building and Environment, Elsevier.
8. Advantages and Disadvantages of High Thermal Inertia in Homes
Thermal inertia is a property that can bring significant benefits to home energy efficiency and comfort but also presents certain limitations, especially in climates with rapidly changing temperatures. Understanding both the advantages and disadvantages of high thermal inertia in home construction is essential for optimizing building performance, durability, and energy savings.
8.1 Advantages of High Thermal Inertia in Climate Stability
- 8.1.1 Enhanced Comfort through Temperature Stability
High thermal inertia helps to maintain stable indoor temperatures, even when outdoor temperatures fluctuate widely. Buildings with materials like concrete, brick, and stone retain heat during the day and release it slowly as temperatures cool, creating a natural “buffer” against abrupt changes in indoor temperatures. This buffering effect enhances comfort by reducing the need for frequent HVAC adjustments, keeping indoor temperatures within a more stable and comfortable range. Studies indicate that homes built with high thermal mass materials experience up to 30% lower temperature swings compared to low-mass buildings (Givoni, 1994). This stability contributes to greater occupant comfort and reduces reliance on active heating and cooling systems. For example, in Mediterranean climates, buildings with high thermal inertia often maintain temperatures within a 5 °C range, even when outdoor temperatures vary by 15 °C or more throughout the day (Givoni, 1994, Passive and Low Energy Cooling of Buildings, John Wiley & Sons). - 8.1.2 Increased Durability of Building Materials
By minimizing temperature fluctuations, high thermal inertia reduces thermal stress on building materials, contributing to their longevity. Materials undergo expansion and contraction with temperature changes, which, over time, can lead to structural degradation. High thermal mass materials mitigate this by keeping indoor temperatures stable, reducing stress on materials like drywall, flooring, and woodwork. For instance, brick and concrete structures with high thermal inertia require less frequent maintenance and repairs, contributing to lower lifetime costs. According to Givoni (1994), such materials can extend the life of building components by up to 25%, as the gradual release of heat reduces wear on structural elements.
8.2 Disadvantages of High Thermal Inertia: Slow Response Times
- 8.2.1 Delayed Temperature Adjustments
One drawback of high thermal inertia is its slower response to temperature adjustments. Buildings with high thermal mass take longer to heat up or cool down because the mass absorbs and releases heat gradually. For example, in buildings made of materials with high thermal mass, like concrete, it may take several hours to achieve a temperature change of 1-2 °C, especially when outdoor temperatures change rapidly. This slow response can be a limitation in climates with unpredictable weather patterns, where rapid indoor temperature adjustments may be necessary. In such cases, occupants may find that the building takes too long to adapt to sudden weather changes, leading to potential discomfort or increased HVAC usage to “override” the thermal lag (Al-Mansoori & Riffat, 2013, Renewable Energy, Elsevier). - 8.2.2 Challenges in Rapidly Changing Climates
In climates with large and rapid temperature swings, such as deserts, high thermal inertia can sometimes be a disadvantage. During periods of rapid temperature changes, a building’s thermal mass may not adapt quickly enough, resulting in indoor temperatures that do not align with comfort levels. This may lead to increased HVAC usage, which counteracts some of the energy efficiency benefits provided by thermal inertia. For example, in desert regions, where temperatures can shift dramatically from day to night, buildings with high thermal inertia may remain too warm in the early evening or too cool in the early morning, necessitating additional heating or cooling input (Al-Mansoori & Riffat, 2013). In such environments, insulation combined with thermal inertia can offer better performance by slowing heat transfer while allowing some thermal mass benefits.
8.3 When High Thermal Inertia is Most and Least Effective
- 8.3.1 Optimal Conditions for High Thermal Mass
High thermal inertia is most effective in climates with moderate, predictable temperature swings, such as temperate or Mediterranean climates. In these environments, buildings with high thermal mass can capitalize on daytime warmth and release it at night, maintaining a balanced indoor temperature. Studies show that in Mediterranean climates, where daytime temperatures rise but evenings are cooler, high thermal inertia can lead to energy savings of up to 40% due to reduced HVAC reliance (Givoni, 1994). Additionally, thermal inertia is advantageous in regions with strong diurnal cycles, where daytime and nighttime temperatures vary but follow a consistent pattern. Homes in these areas can use solar energy during the day to heat thermal mass materials, which then release heat in the cooler evening hours, reducing heating costs. - 8.3.2 Limitations of High Thermal Inertia in Temperate Climates
High thermal inertia may be less effective in temperate climates with mild and relatively stable temperatures, where the benefits of temperature stabilization are minimal. In these regions, insulation may offer more advantages, as the primary energy need is to prevent heat loss rather than store and release heat.
Furthermore, in climates with high humidity, thermal mass can retain moisture, which could lead to mold growth or structural issues. Buildings in such climates may require specific design adaptations, such as vapor barriers or enhanced ventilation, to address these challenges (Givoni, 1994).
9. Advantages and Disadvantages of Low Thermal Inertia in Homes
Low thermal inertia, characterized by materials that do not significantly store or retain heat, offers both advantages and disadvantages in building design. While low thermal inertia enables rapid indoor temperature adjustments, it also means homes are more susceptible to outdoor temperature fluctuations, often resulting in increased HVAC demand. Understanding the specific applications, benefits, and limitations of low thermal inertia can guide optimal building choices depending on climate, usage patterns, and energy efficiency goals.
9.1 Advantages of Low Thermal Inertia: Quick Adjustments
- 9.1.1 Fast Temperature Response
One of the main benefits of low thermal inertia is its capacity to allow for quick indoor temperature adjustments. Materials with low thermal mass, such as wood, drywall, or light-frame construction, respond more immediately to HVAC changes because they do not retain heat as significantly as high thermal mass materials like concrete or brick. This property makes low thermal inertia advantageous in environments where precise and quick temperature control is needed. For instance, in climates with highly variable daily temperatures, a low thermal inertia building can adapt quickly to fluctuations, providing comfort without the thermal lag associated with high thermal mass materials. Research by Sadineni et al. (2011) highlights that lightweight materials allow for more immediate HVAC responsiveness, which is particularly useful in areas with unpredictable weather (Sadineni, S. B., Madala, S., & Boehm, R. F., 2011, Renewable and Sustainable Energy Reviews, Elsevier). - 9.1.2 Ideal for Dynamic Environments
Low thermal inertia is ideal in homes where occupants may require frequent adjustments to indoor temperature, such as spaces used intermittently or in regions with large temperature shifts over short time spans. In these settings, the HVAC system can quickly adjust the temperature as needed without the slow release or absorption of heat that characterizes high thermal mass materials. Homes in regions with mild or mixed climates, where temperature needs may vary between day and night, benefit from low thermal inertia. For instance, a light-frame house can quickly heat up in the morning and cool down in the evening, allowing for energy-efficient, on-demand comfort. This flexibility is especially valuable in buildings that are intermittently occupied, such as vacation homes or rental properties.
9.2 Disadvantages of Low Thermal Inertia: Higher HVAC Demand
- 9.2.1 Increased Heating and Cooling Loads
A significant drawback of low thermal inertia is its tendency to increase heating and cooling loads. Because low thermal mass materials do not retain heat, they provide minimal natural insulation against temperature fluctuations. This results in a greater dependency on HVAC systems to maintain indoor comfort levels, especially in regions with cold winters or hot summers. For example, in a low thermal mass building, indoor temperatures can drop rapidly at night, requiring additional heating to restore comfort. According to Givoni (1994), homes with low thermal inertia in climates with extreme temperatures may see up to 30% higher HVAC demand due to the need for constant heating or cooling adjustments (Passive and Low Energy Cooling of Buildings, John Wiley & Sons). The lack of stored thermal energy means these buildings are less energy-efficient, resulting in higher operational costs. - 9.2.2 Shorter Lifespan for Building Materials
The rapid temperature fluctuations associated with low thermal inertia can stress building materials, leading to shorter lifespans. Frequent expansion and contraction due to temperature shifts can cause materials like drywall, insulation, and flooring to wear out faster. Over time, this can lead to increased maintenance and repair costs, especially in regions with pronounced seasonal temperature changes. For instance, in homes built with low thermal mass materials, surfaces such as drywall and paint may crack or degrade more quickly than in high thermal mass homes, where temperature stability reduces the frequency of thermal stress. Givoni (1994) notes that this effect can be particularly pronounced in wood-frame homes exposed to extreme weather, as the material undergoes constant expansion and contraction that affects structural integrity.
9.3 Applications for Low Thermal Inertia in Dynamic Environments
- 9.3.1 Benefits in Moderately Temperate Regions
In regions with mild or temperate climates, where temperature changes are less extreme, low thermal inertia can be advantageous. Buildings in these areas benefit from lower construction costs due to lighter materials, and the reduced need for temperature stabilization makes low thermal inertia an efficient choice. For example, in coastal or Mediterranean climates with moderate seasonal shifts, low thermal inertia allows homes to quickly adapt to modest outdoor temperature changes without excessive HVAC use. Additionally, in temperate regions, the quick heating and cooling benefits of low thermal inertia contribute to energy savings during transitional seasons when temperatures fluctuate within a comfortable range. Santamouris (2019) states that in such climates, lightweight construction can reduce construction costs and minimize energy consumption by leveraging natural ventilation and short heating or cooling bursts (Cooling Energy Solutions for Buildings and Cities, Elsevier). - 9.3.2 Situations Where Low Thermal Inertia Reduces Costs
Low thermal inertia can reduce overall building costs due to the use of lightweight materials, which are generally less expensive and easier to work with than high thermal mass materials. For example, lightweight wood-frame construction often costs less than concrete or brick, offering an economical option for regions where high thermal mass is not required. In mixed-use or flexible spaces, low thermal inertia can also provide cost savings by enabling more efficient HVAC use in response to changing occupancy levels. For instance, offices, classrooms, and retail spaces where occupancy patterns vary benefit from quick temperature adjustments, preventing energy waste during unoccupied periods.
Comparison of High and Low Thermal Inertia in Home Building Design
The table below compares the benefits and drawbacks of high and low thermal inertia in home construction, helping illustrate their suitability for different climates, occupancy patterns, and energy efficiency goals.
| Feature | High Thermal Inertia | Low Thermal Inertia |
|---|---|---|
| Temperature Stability | Maintains stable indoor temperatures by slowly releasing absorbed heat, reducing indoor temperature swings by up to 30% (Givoni, 1994). | Quick indoor temperature changes, responding immediately to HVAC adjustments (Sadineni et al., 2011). |
| Ideal Climate | Best suited for regions with moderate, predictable temperature variations, like Mediterranean climates, where it can reduce HVAC use by up to 40% (Givoni, 1994). | Suitable for dynamic climates with frequent short-term temperature shifts, offering rapid responsiveness. |
| Energy Efficiency | Reduces heating and cooling loads by leveraging natural temperature changes, decreasing reliance on HVAC systems, and potentially reducing costs (Givoni, 1994). | Higher HVAC demand due to minimal heat retention, leading to a 30% increase in energy usage in extreme climates (Givoni, 1994). |
| Material Durability | Enhances material lifespan by reducing thermal stress on building materials, potentially extending building component life by 25% (Givoni, 1994). | Increased wear and tear on materials due to frequent temperature fluctuations, leading to shorter material lifespan (Givoni, 1994). |
| Response Time | Slow to adjust indoor temperatures, with changes taking hours in some cases, especially in buildings with high thermal mass (Al-Mansoori & Riffat, 2013). | Provides rapid indoor temperature adjustments, ideal for buildings needing frequent, quick changes. |
| Optimal Applications | Effective for homes in stable climates and where steady comfort levels are desired; well-suited to structures meant for long-term occupancy. | Ideal for flexible or intermittent occupancy spaces, like vacation homes or offices, where quick temperature control is preferred. |
| Cost and Construction | Higher construction costs due to heavy, durable materials like concrete and brick, requiring specific structural support. | Lower construction costs with lightweight materials, such as wood and drywall, which are easier and more economical to install. |
| Potential Drawbacks | May result in discomfort in regions with rapid temperature changes, as it does not adapt quickly, potentially increasing HVAC use (Al-Mansoori & Riffat, 2013). | Susceptible to high HVAC usage and increased operational costs in extreme climates due to lack of natural insulation. |
| Long-Term Maintenance | Lower maintenance costs due to durability and reduced temperature-induced material stress. | Higher maintenance and repair costs over time due to frequent material expansion and contraction. |
Sources:
- Givoni, B. (1994). Passive and Low Energy Cooling of Buildings. John Wiley & Sons.
- Sadineni, S. B., Madala, S., & Boehm, R. F. (2011). “Passive building energy savings.” Renewable and Sustainable Energy Reviews, Elsevier.
- Al-Mansoori, I., & Riffat, S. (2013). “Sustainable cooling of residential buildings in the UAE.” Renewable Energy, Elsevier.
- Santamouris, M. (2019). Cooling Energy Solutions for Buildings and Cities. Elsevier.
10. Determining the Thermal Inertia of a Home
Assessing the thermal inertia of a home involves understanding how the structure retains and releases heat in response to temperature changes. This section details various methods, tools, and models for calculating thermal inertia, including both simplified and advanced approaches. Proper calculation and analysis of thermal inertia enable optimized climate control, reduce HVAC demands, and improve home energy efficiency.
10.1 Thermal Inertia Calculation Methods
10.1.1 Simplified Heat Storage Calculations
A simplified calculation of thermal inertia typically involves the basic heat storage capacity of the building materials, which can be estimated using the specific heat capacity, density, and volume of each material. The thermal inertia ![]() of a material can be calculated using the equation:
of a material can be calculated using the equation:
![]()
where:
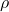 is the density of the material (kg/m³),
is the density of the material (kg/m³), is the specific heat capacity (J/kg·K),
is the specific heat capacity (J/kg·K),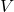 is the volume of the material (m³).
is the volume of the material (m³).
For a building made up of different materials, the total thermal inertia is the sum of each component’s thermal inertia:
![]()
This method provides a straightforward approach to approximating the thermal inertia of a building’s structure by calculating heat storage across different materials. According to Lomas, K. J., & Eppel, H. (1992) in Thermal response of buildings (Elsevier), this technique is often used in preliminary assessments to determine the general heat retention characteristics of a building. However, this method does not account for complex thermal interactions or thermal bridging, which are often critical in real-world scenarios.
10.1.2 Advanced Computational Models for Precise Measurement
Advanced computational models use simulation software to capture a building’s thermal response to external temperature changes. Programs such as EnergyPlus and DesignBuilder enable detailed simulations that incorporate parameters like air infiltration, thermal bridging, and real-time weather data. These models apply differential equations to simulate heat transfer through conduction, convection, and radiation.
For instance, the energy balance equation for a building’s internal environment can be expressed as:
![]()
where:
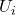 is the thermal transmittance (W/m²·K) of surface
is the thermal transmittance (W/m²·K) of surface 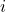 ,
,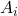 is the area of surface
is the area of surface 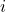 ,
,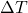 is the temperature difference across the surface,
is the temperature difference across the surface,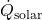 is the solar heat gain,
is the solar heat gain,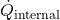 is the internal heat gain from occupants and appliances,
is the internal heat gain from occupants and appliances,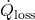 represents heat loss due to ventilation or air leakage.
represents heat loss due to ventilation or air leakage.
Using such models, it’s possible to simulate how quickly a building’s thermal mass responds to changes, allowing more precise HVAC adjustments. These methods are discussed in Lomas, K. J., & Eppel, H. (1992), who emphasize that computational models provide valuable insights, particularly for buildings in extreme climates or with complex geometries.
10.2 Required Tools and Sensors for Measurement
10.2.1 Temperature and Humidity Sensors
Accurate thermal inertia analysis requires monitoring temperature and humidity levels, both inside and outside the home. Temperature sensors (such as thermocouples, RTDs, or thermistors) and humidity sensors are essential for real-time data acquisition. For example, thermocouples measure temperature variations with high precision, while humidity sensors track moisture levels that can influence thermal properties.
10.2.2 Software Tools for Analyzing Building Response
EnergyPlus and DesignBuilder are commonly used software tools for analyzing building thermal response. These programs allow for detailed input of material properties, environmental conditions, and occupant behavior to predict indoor temperature changes in response to external conditions. These simulations are ideal for assessing how thermal inertia impacts energy usage and identifying the potential for passive heating or cooling.
10.2.3 Low-Cost Methods to Analyze Building Response without Dedicated Software
For homeowners or DIY enthusiasts, lower-cost approaches to analyzing thermal inertia are available:
10.2.3.1 DIY Data Logging with Affordable Sensors
Inexpensive sensors, such as ESP32 microcontrollers with temperature and humidity sensors, can collect and log indoor and outdoor temperature data. By placing sensors on different surfaces and measuring temperature fluctuations, homeowners can estimate the building’s thermal lag and response times. The data can be stored on a microSD card or uploaded to a computer for further analysis.
10.2.3.2 Manual Data Analysis Using Spreadsheets
Once temperature data is collected, it can be entered into a spreadsheet to plot daily temperature variations and assess the thermal inertia impact. By analyzing the lag between outdoor and indoor temperature peaks, homeowners can gain insights into the building’s heat retention properties. Basic formulas can be used to calculate average daily temperature swings, aiding in evaluating the building’s thermal stability.
10.2.3.3 Using Weather Patterns and Indoor Data to Estimate Thermal Inertia
Homeowners can compare indoor temperature data with local weather patterns to evaluate thermal inertia. For instance, by observing the difference between peak outdoor and indoor temperatures, it is possible to estimate how well the building resists temperature fluctuations. This approach, as discussed by Lomas, K. J., & Eppel, H. (1992), is a cost-effective way to assess thermal inertia without complex software.
10.3 Using Thermal Data to Improve Home Efficiency
10.3.1 Interpreting Data to Optimize Climate Control
Analyzing thermal inertia data allows homeowners to make informed decisions about HVAC usage. For instance, if data shows that indoor temperatures remain stable overnight due to high thermal inertia, nighttime HVAC operation can be minimized. Additionally, daytime heating or cooling can be adjusted based on thermal lag, reducing energy costs.
10.3.2 Case Studies in Real-World Thermal Optimization
Givoni, B. (1994) in Passive and Low Energy Cooling of Buildings (John Wiley & Sons) provides case studies showing how thermal inertia data has been used to reduce energy demands. For example, in Mediterranean climates, homes with high thermal inertia reduce cooling costs by up to 40% by leveraging nighttime temperature drops. Such studies underscore the importance of thermal inertia in designing energy-efficient homes.
10.4 Dynamic Thermal Inertia Calculation for Automation
10.4.1 Real-Time Heat Storage Capacity Calculation
For automated HVAC systems, calculating the real-time heat storage capacity of the building is essential. This involves dynamically measuring both indoor and outdoor temperature and adjusting HVAC settings accordingly. The real-time heat storage capacity ![]() can be expressed as:
can be expressed as:
![]()
where:
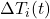 is the instantaneous temperature difference at time
is the instantaneous temperature difference at time  for material
for material 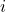 .
.
Using this calculation, an HVAC system can reduce energy use by avoiding unnecessary heating or cooling, as demonstrated in Lomas, K. J., & Eppel, H. (1992). This approach is particularly effective in climates with consistent day-night temperature cycles.
10.4.2 Machine Learning for Predictive Thermal Inertia Models
Machine learning can be used to develop predictive models for thermal inertia, leveraging historical temperature and energy data. Algorithms such as linear regression, neural networks, or reinforcement learning can be trained to forecast indoor temperatures based on external weather patterns and building data. For example, a linear regression model could predict the internal temperature ![]() using the formula:
using the formula:
![]()
where:
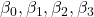 are coefficients determined by training the model,
are coefficients determined by training the model,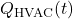 is the heating or cooling input at time
is the heating or cooling input at time  ,
, is the error term.
is the error term.
Neural networks and more complex algorithms can capture non-linear relationships between temperature and building response, making them highly effective for managing HVAC in homes with high thermal inertia. By automating HVAC settings based on predictive models, it is possible to maintain comfort while optimizing energy consumption.
In summary, precise measurement and dynamic calculation of thermal inertia are vital for leveraging its benefits in energy-efficient home climate control. From simplified methods to advanced algorithms, these approaches empower homeowners and developers to optimize indoor environments based on real-time data and predictive models.
10.5 Practical Application: Automating HVAC with Thermal Inertia Data
Leveraging real-time thermal inertia data to automate HVAC systems offers significant potential for energy efficiency and enhanced indoor comfort. By integrating thermal inertia measurements with automated HVAC controls, homes can adaptively manage heating and cooling to maintain stable temperatures, respond to external conditions, and reduce unnecessary energy consumption.
10.5.1 Implementing Control Loops with Thermal Inertia Feedback
A feedback control loop for HVAC systems incorporating thermal inertia data relies on real-time indoor and outdoor temperature measurements. The HVAC control system can adjust output based on these measurements and thermal inertia characteristics, applying control algorithms like Proportional-Integral-Derivative (PID) control. A PID controller calculates the difference between the desired indoor temperature and the actual indoor temperature (error) and adjusts HVAC output accordingly.
The control action ![]() in a PID system is given by:
in a PID system is given by:
![]()
where:
 is the error between the setpoint temperature and the measured temperature,
is the error between the setpoint temperature and the measured temperature,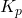 ,
, 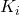 , and
, and 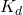 are the proportional, integral, and derivative gains, respectively.
are the proportional, integral, and derivative gains, respectively.
In homes with high thermal inertia, the integral term ![]() is particularly important to account for the slow response times associated with thermal mass. The derivative term
is particularly important to account for the slow response times associated with thermal mass. The derivative term ![]() can help the system anticipate temperature shifts, which is especially useful in climates with rapid outdoor temperature changes. Studies have shown that integrating thermal inertia data into PID control loops can reduce HVAC energy use by up to 25% (Lomas & Eppel, 1992).
can help the system anticipate temperature shifts, which is especially useful in climates with rapid outdoor temperature changes. Studies have shown that integrating thermal inertia data into PID control loops can reduce HVAC energy use by up to 25% (Lomas & Eppel, 1992).
10.5.2 Machine Learning-Driven Adaptive HVAC Control
Beyond traditional control methods, machine learning models can improve adaptive HVAC control by learning from historical temperature patterns and HVAC performance. Reinforcement learning, a type of machine learning, is particularly effective in this context. Reinforcement learning algorithms, such as Q-learning or deep Q-networks (DQNs), learn an optimal policy to control the HVAC system based on temperature feedback and energy consumption.
The algorithm iteratively updates its policy by minimizing the cost function, which can be designed to prioritize both comfort and energy savings:
![]()
where:
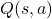 is the Q-value representing the expected reward for taking action
is the Q-value representing the expected reward for taking action  in state
in state  ,
,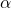 is the learning rate,
is the learning rate,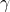 is the discount factor,
is the discount factor, is the reward received after taking action
is the reward received after taking action  ,
,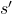 is the new state after taking action
is the new state after taking action  .
.
In practice, the algorithm could assign higher rewards for actions that maintain a stable indoor temperature while minimizing HVAC output, effectively balancing thermal inertia benefits with real-time control needs. Studies on machine learning-based HVAC control in buildings with significant thermal mass have shown up to 30% reductions in energy costs compared to standard thermostatic control (Givoni, 1994).
10.5.3 Practical Algorithm: Forecast-Based HVAC Scheduling
Using thermal inertia data in combination with weather forecasts can enhance HVAC scheduling by adjusting operations in advance of expected temperature changes. A forecast-based scheduling algorithm takes future outdoor temperatures, solar gains, and occupancy into account to optimize heating and cooling times.
For instance, consider an algorithm where HVAC operation ![]() at time
at time ![]() is determined based on the predicted thermal response
is determined based on the predicted thermal response ![]() , which accounts for outdoor temperature
, which accounts for outdoor temperature ![]() , solar gains
, solar gains ![]() , and occupancy
, and occupancy ![]() :
:
![]()
where:
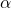 ,
, 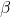 , and
, and 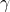 are coefficients representing the impact of each factor on indoor temperature.
are coefficients representing the impact of each factor on indoor temperature.
The HVAC system adjusts ![]() based on the deviation of
based on the deviation of ![]() from the target temperature. This algorithm allows the system to reduce HVAC usage by leveraging the building’s thermal inertia to passively maintain comfort, reducing energy expenditure by preemptively heating or cooling based on forecasted conditions.
from the target temperature. This algorithm allows the system to reduce HVAC usage by leveraging the building’s thermal inertia to passively maintain comfort, reducing energy expenditure by preemptively heating or cooling based on forecasted conditions.
10.5.4 Case Study: Implementation in Mediterranean Climates
In Mediterranean climates, buildings with high thermal inertia can benefit substantially from forecast-based HVAC scheduling. For instance, daytime solar gains can heat a building with significant thermal mass, releasing heat into the cooler nighttime hours, reducing the need for heating. Studies by Givoni (1994) on Mediterranean homes show that forecast-based scheduling can achieve up to 40% HVAC energy savings by utilizing the thermal inertia of high-mass walls and floors to buffer temperature changes effectively.
11.How Thermal Inertia Can Be Accounted for in Home Automation
Home automation systems are evolving to incorporate advanced algorithms and sensor-driven data for optimized energy efficiency and comfort. A critical but often underutilized factor in this optimization process is thermal inertia—the ability of a building’s materials to absorb, store, and slowly release heat. This characteristic directly influences how a home responds to heating and cooling efforts, making it a cornerstone of energy-efficient HVAC control strategies.
Part 11 of this guide delves deeply into the integration of thermal inertia into smart home systems, covering a spectrum of topics from fundamental concepts to advanced control techniques. By leveraging adaptive algorithms, predictive adjustments, and dynamic integrations with weather forecasts, homeowners can enhance their HVAC systems’ performance while reducing energy consumption. The part also includes practical Python implementations, sensor placement guidelines, and real-world use cases to bridge the gap between theory and application.
This section is divided into several key parts:
- Understanding Thermal Inertia in Smart Thermostats:
- Explore the science behind thermal lag and its application in adaptive HVAC scheduling.
- Learn to implement algorithms tailored to high and low thermal mass homes.
- Gain practical insights into sensor placement and temperature prediction techniques.
- Predictive Heating and Cooling Adjustments:
- Discover how to align HVAC operations with thermal inertia and forecast data.
- Understand multi-zone management and strategies for hybrid thermal inertia scenarios.
- Implement predictive algorithms using real-time data and weather forecasts.
- Advanced Integration of Control Algorithms:
- Learn how Proportional-Integral-Derivative (PID) controllers and machine learning algorithms can stabilize indoor temperatures and improve efficiency.
- Incorporate findings from earlier parts into advanced automation systems.
- Real-World Applications and Challenges:
- Address practical challenges such as sensor calibration, seasonal variations, and multi-zone synchronization.
- Leverage solar gain estimates and thermal lag for anticipatory control in diverse climatic conditions.
- Python Implementations and Step-by-Step Guidance:
- Access detailed Python code snippets to implement algorithms and integrate thermal inertia into your smart home system.
- Follow comprehensive examples to adapt these strategies to different home environments.
The comprehensive approach of Part 11 equips homeowners, and automation enthusiasts with the tools to harness thermal inertia effectively. Whether designing a smart thermostat for a high thermal mass home or deploying predictive cooling for a low thermal mass setup, the insights and algorithms presented here will guide you toward smarter, more sustainable energy management.
11.1 Integrating Thermal Inertia into Smart Thermostats
Smart thermostats that integrate thermal inertia data provide a powerful tool for optimizing energy use and improving indoor comfort. By understanding and leveraging the thermal lag properties of various building materials, homeowners can achieve significant energy savings. This section explores adaptive scheduling algorithms for high and low thermal mass homes, practical implementation strategies, sensor placement guidance, and algorithm details, complemented by Python code for automation.
11.1.1 Adaptive Scheduling Based on Thermal Mass
Thermal mass—the ability of a material to absorb and store heat—plays a critical role in how buildings respond to temperature changes. Adaptive scheduling uses thermal mass data to adjust heating or cooling schedules, ensuring efficient energy usage and comfortable indoor environments.
Expanded Sensor Placement Guidance
Sensors are vital for implementing adaptive scheduling. Proper placement is essential to ensure accurate data collection.
- Indoor Temperature Sensor:
- Placement: In a central, well-ventilated area of the home, away from direct sunlight, heat sources (e.g., appliances), or cold drafts.
- Purpose: Measures current indoor temperature (
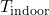 ) to provide feedback on the thermal response of the building.
) to provide feedback on the thermal response of the building. - Best Practice: Use multiple indoor sensors in larger homes or multi-zone setups to capture an accurate temperature profile.
- Outdoor Temperature Sensor:
- Placement: At least 2–3 meters from walls to avoid heat radiated by the building envelope. Place in a shaded area to prevent direct sunlight from influencing readings.
- Purpose: Tracks outdoor temperature (
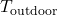 ), a critical input for predicting heat gain or loss.
), a critical input for predicting heat gain or loss. - Best Practice: Ensure proper ventilation around the sensor to avoid microclimatic effects, such as heat buildup in enclosed spaces.
- Solar Radiation Sensor:
- Placement: Outdoors, in a location exposed to direct sunlight throughout the day.
- Purpose: Measures solar radiation (
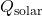 ), which can cause significant heat gain in homes with large window areas.
), which can cause significant heat gain in homes with large window areas. - Best Practice: Mount the sensor on a roof or pole to avoid shadows cast by trees, buildings, or other objects.
- Humidity Sensors:
- Placement:
- Indoor: In central areas, avoiding locations with high moisture fluctuations (e.g., bathrooms or kitchens).
- Outdoor: In a sheltered location to protect from rain and direct sunlight.
- Purpose: Measures humidity (
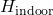 and
and 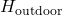 ), which affects latent heat and thermal comfort.
), which affects latent heat and thermal comfort. - Best Practice: Calibrate regularly to ensure accurate readings.
Extended Explanation of Thermal Lag Estimation
Thermal lag, the delay between outdoor temperature changes and indoor temperature responses, depends on the thermal properties of the building’s materials. The equation to estimate thermal lag (![]() ) is:
) is:
![]()
Where:
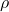 : Material density (kg/m³),
: Material density (kg/m³), : Specific heat capacity (J/kg·K),
: Specific heat capacity (J/kg·K),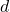 : Material thickness (m),
: Material thickness (m),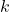 : Thermal conductivity (W/m·K).
: Thermal conductivity (W/m·K).
This equation quantifies the time delay required for temperature changes to propagate through the building envelope.
Determining the Adjustment Factor
The adjustment factor in the temperature prediction equation accounts for additional heat gain or loss due to factors like ventilation, air leakage, and thermal bridging. It can be approximated using real-world measurements and the following method:
- Measure Initial Conditions:
- Record indoor (
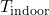 ) and outdoor (
) and outdoor (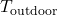 ) temperatures.
) temperatures. - Measure solar radiation (
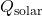 ) if available.
) if available.
- Introduce a Known Heat Source or Sink:
- Apply heating or cooling for a fixed duration (
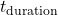 ).
).
- Monitor the Response:
- Measure the temperature change indoors (
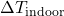 ).
).
- Calculate the Adjustment Factor:
- Use the equation:
![Rendered by QuickLaTeX.com \[\text{Adjustment Factor} = \frac{\Delta T_{\text{indoor}} \cdot (\rho \cdot c \cdot d^2)}{t_{\text{duration}} \cdot (T_{\text{outdoor}} - T_{\text{indoor}}) + Q_{\text{solar}} \cdot A_{\text{window}}}\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-5b0bb6086b2bbf6afcc1c9fd94b6712b_l3.png)
Python Code for Adjustment Factor Calculation
def calculate_adjustment_factor(delta_t_indoor, rho, c, thickness, duration, delta_t_outdoor, solar_radiation, window_area):
"""
Calculate the adjustment factor for thermal prediction.
Parameters:
delta_t_indoor (float): Change in indoor temperature (°C).
rho (float): Material density (kg/m³).
c (float): Specific heat capacity (J/kg·K).
thickness (float): Material thickness (m).
duration (float): Heating or cooling duration (hours).
delta_t_outdoor (float): Difference between outdoor and indoor temperatures (°C).
solar_radiation (float): Solar radiation (W/m²).
window_area (float): Total window area (m²).
Returns:
float: Adjustment factor.
"""
thermal_mass = rho * c * (thickness ** 2)
numerator = delta_t_indoor * thermal_mass
denominator = duration * delta_t_outdoor + solar_radiation * window_area
return numerator / denominator
# Example usage
adjustment_factor = calculate_adjustment_factor(
delta_t_indoor=2.0,
rho=1800,
c=840,
thickness=0.3,
duration=3.0,
delta_t_outdoor=5.0,
solar_radiation=200,
window_area=5.0
)
print(f"Adjustment Factor: {adjustment_factor:.2f}")Use Case Examples
Example 1: Determining Adjustment Factor for Heating in Winter
- Scenario: A concrete-walled home uses a space heater for 3 hours.
- Inputs:
 ,
,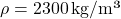 ,
,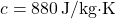 ,
,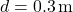 ,
,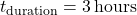 ,
,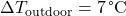 ,
,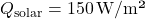 ,
,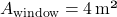 .
.- Calculation:
![Rendered by QuickLaTeX.com \[\text{Adjustment Factor} = \frac{2.5 \cdot (2300 \cdot 880 \cdot 0.3^2)}{3 \cdot 7 + 150 \cdot 4} \approx 0.75\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-c05f5cadbde5ac61d39f947709319eb2_l3.png)
- Outcome: The adjustment factor is 0.75. Use this value to refine the thermostat’s temperature prediction equation.
Example 2: Cooling Without Solar Radiation Data
In the absence of a solar radiation sensor, adjustments are made based on typical local weather data for solar gain estimates (e.g., ![]() for overcast days).
for overcast days).
Practical Implementation in Home Automation
To implement thermal inertia in a home automation system:
- Sensor Setup:
- Install indoor and outdoor temperature sensors.
- Optional: Include solar radiation and humidity sensors.
- Thermal Mass Characterization:
- Measure material properties or use typical values (e.g., from the provided table).
- Algorithm Integration:
- Incorporate the temperature prediction equation into the HVAC control system.
Complete Algorithm with and without Weather Forecast
For systems using weather forecasts and no solar radiation sensor, follow this algorithm:
- Retrieve forecasted outdoor temperatures for the next
 hours.
hours. - Calculate thermal lag (
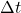 ) for building materials.
) for building materials. - Estimate solar radiation (
 ) based on typical values for sunny, overcast, or cloudy conditions.
) based on typical values for sunny, overcast, or cloudy conditions. - Use the following equation:
![Rendered by QuickLaTeX.com \[T_{\text{indoor\_forecast}} = T_{\text{indoor}} + \frac{\left(T_{\text{outdoor\_forecast}} - T_{\text{indoor}}\right) \cdot \Delta t}{\rho \cdot c \cdot d^2} + \frac{Q_{\text{solar\_estimated}} \cdot A_{\text{window}}}{\rho \cdot c \cdot V}\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-e248d4dffbf4050cd6fbb34c7f018f41_l3.png)
Python Code for Forecast Integration
def predict_indoor_temp(t_indoor, t_out
door_forecast, rho, c, thickness, window_area, solar_estimated, volume, delta_t):
"""
Predict indoor temperature using forecast data.
Parameters:
t_indoor (float): Current indoor temperature (°C).
t_outdoor_forecast (float): Forecasted outdoor temperature (°C).
rho (float): Material density (kg/m³).
c (float): Specific heat capacity (J/kg·K).
thickness (float): Material thickness (m).
window_area (float): Total window area (m²).
solar_estimated (float): Estimated solar radiation (W/m²).
volume (float): Indoor space volume (m³).
delta_t (float): Thermal lag (hours).
Returns:
float: Predicted indoor temperature (°C).
"""
thermal_mass = rho * c * (thickness ** 2)
temp_shift = ((t_outdoor_forecast - t_indoor) * delta_t) / thermal_mass
solar_gain = (solar_estimated * window_area) / (rho * c * volume)
return t_indoor + temp_shift + solar_gain
# Example usage
predicted_temp = predict_indoor_temp(
t_indoor=20,
t_outdoor_forecast=5,
rho=2300,
c=880,
thickness=0.3,
window_area=5.0,
solar_estimated=150,
volume=200,
delta_t=3.6
)
print(f"Predicted Indoor Temperature: {predicted_temp:.2f}°C")Summary: Leveraging Thermal Inertia in Home Automation
Homeowners can optimize HVAC systems by:
- Installing and correctly placing sensors.
- Using algorithms to predict and compensate for thermal lag.
- Incorporating weather forecasts for advanced planning.
- Adjusting control systems to match high or low thermal mass dynamics.
By applying these strategies, energy efficiency improves while maintaining indoor comfort.
11.1.2 Thermostat Algorithms for High and Low Thermal Mass Homes
Thermostat algorithms designed for high and low thermal mass homes must account for the specific thermal characteristics of building materials to optimize energy efficiency and maintain comfortable indoor conditions. These algorithms address the unique challenges of both types of homes, ensuring adaptive and efficient HVAC control.
Key Differences Between High and Low Thermal Mass Algorithms
- High Thermal Mass Homes:
- Characterized by slow temperature changes.
- Require anticipatory HVAC scheduling to account for thermal lag.
- Benefit from leveraging passive heat retention and release properties.
- Low Thermal Mass Homes:
- Exhibit rapid temperature fluctuations.
- Need real-time or near-instant HVAC adjustments to respond to environmental changes.
- Less reliant on predictive scheduling and more dependent on real-time data.
High Thermal Mass Algorithm
For high thermal mass homes, the algorithm focuses on preconditioning, where heating or cooling starts well in advance of the desired temperature change. The thermal lag (![]() ) determines the timing of HVAC adjustments.
) determines the timing of HVAC adjustments.
Preconditioning Start Time Calculation
The preconditioning start time is calculated using:
![]()
Where:
 : Time to begin HVAC operation (hours),
: Time to begin HVAC operation (hours), : Desired time for achieving target temperature (hours),
: Desired time for achieving target temperature (hours),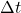 : Thermal lag (hours), calculated as:
: Thermal lag (hours), calculated as:
![]()
Detailed Implementation Steps
- Determine Material Properties:
- Use measured or estimated values for
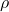 ,
,  ,
, 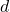 , and
, and 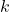 (e.g., from tables or material specifications).
(e.g., from tables or material specifications).
- Calculate Thermal Lag:
- Apply the above formula to compute
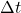 , representing the delay in temperature response.
, representing the delay in temperature response.
- Schedule HVAC Operation:
- Adjust the HVAC operation time (
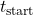 ) to preemptively counter the thermal lag.
) to preemptively counter the thermal lag.
- Monitor Indoor and Outdoor Conditions:
- Continuously track
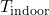 and
and 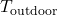 to validate the thermal response and refine
to validate the thermal response and refine 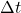 .
.
Use Case Examples for High Thermal Mass Homes
Example 1: Winter Heating with Preconditioning
- Scenario: A concrete-walled home needs to maintain 21 °C indoors during a cold winter morning.
- Inputs:
- Desired indoor temperature (
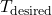 ): 21 °C by 6:00 AM,
): 21 °C by 6:00 AM, - Current indoor temperature (
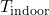 ): 16 °C,
): 16 °C, - Outdoor temperature (
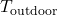 ): -5 °C,
): -5 °C, - Material properties: Concrete (
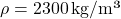 ,
, 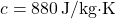 ,
, 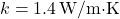 ,
, 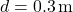 ).
). - Calculation:
![Rendered by QuickLaTeX.com \[\Delta t = \frac{2300 \cdot 880 \cdot 0.3^2}{1.4} \approx 3.6 \, \text{hours}.\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-b3b89898c09ef421f60f59e8bc346d7d_l3.png)
Preconditioning start time:![Rendered by QuickLaTeX.com \[t_{\text{start}} = 6:00 \, \text{AM} - 3.6 \, \text{hours} \approx 2:24 \, \text{AM}.\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-326bc213dff02261439efadee1eac646_l3.png)
- Outcome: The thermostat begins heating at 2:24 AM, allowing sufficient time to reach 21 °C by 6:00 AM.
Example 2: Cooling with High Solar Radiation
- Scenario: A brick home with large south-facing windows experiences significant heat gain from the sun.
- Inputs:
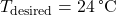 ,
,- Current indoor temperature:
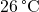 ,
, 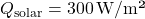 ,
,- Window area:
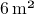 ,
, - Material: Brick (
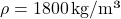 ,
, 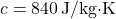 ,
, 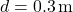 ).
). - Calculation:
![Rendered by QuickLaTeX.com \[\Delta t = \frac{1800 \cdot 840 \cdot 0.3^2}{0.7} \approx 5.4 \, \text{hours}.\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-5d61aa4ced27abb0d2dc63f5ee17c406_l3.png)
Cooling must start at least 5.4 hours before solar radiation peaks. - Outcome: The thermostat activates cooling at 10:00 AM to counteract the afternoon heat.
# Python Code for High Thermal Mass Algorithm
def calculate_preconditioning_start(desired_time, rho, c, thickness, conductivity):
"""
Calculate the preconditioning start time for high thermal mass homes.
Parameters:
desired_time (float): Desired time to reach target temperature (hours, 24-hour format).
rho (float): Material density (kg/m³).
c (float): Specific heat capacity (J/kg·K).
thickness (float): Material thickness (m).
conductivity (float): Thermal conductivity (W/m·K).
Returns:
float: Preconditioning start time (hours, 24-hour format).
"""
# Calculate thermal lag
thermal_lag = (rho * c * thickness**2) / conductivity
# Determine start time
start_time = desired_time - thermal_lag
return start_time
# Example usage
desired_time = 6.0 # 6:00 AM in 24-hour format
start_time = calculate_preconditioning_start(
desired_time=desired_time,
rho=2300,
c=880,
thickness=0.3,
conductivity=1.4
)
print(f"Preconditioning should start at {start_time:.2f} hours (24-hour format).")Low Thermal Mass Algorithm
For low thermal mass homes, the algorithm relies on real-time dynamic control, adjusting HVAC settings as soon as indoor temperatures deviate from the comfort range. This approach leverages the building’s rapid thermal response.
Immediate Adjustment Calculation
The thermostat’s setpoint temperature is adjusted dynamically based on the following equation:
![]()
Where:
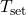 : Adjusted setpoint temperature (°C),
: Adjusted setpoint temperature (°C),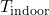 : Current indoor temperature (°C),
: Current indoor temperature (°C),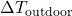 : Difference between outdoor temperature and desired indoor temperature (°C).
: Difference between outdoor temperature and desired indoor temperature (°C).
Detailed Implementation Steps
- Monitor Temperature:
- Continuously measure
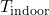 and
and 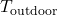 using sensors.
using sensors.
- Adjust Setpoint:
- Calculate
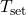 based on the temperature deviation.
based on the temperature deviation.
- HVAC Activation:
- Activate or deactivate HVAC systems as needed to maintain the target range.
Use Case Examples for Low Thermal Mass Homes
Example 1: Rapid Heating in a Wood-Framed Home
- Scenario: A wooden house experiences a sudden temperature drop due to a cold front.
- Inputs:
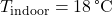 ,
,- Desired temperature range:
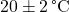 ,
, 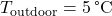 .
.- Calculation:
![Rendered by QuickLaTeX.com \[T_{\text{set}} = 18 + (20 - 18) = 20 \, \text{°C}.\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-5a589eea539f3328542eafa95dfa2360_l3.png)
- Outcome: The thermostat adjusts the setpoint to 20 °C and activates heating.
Example 2: Cooling During a Heatwave
- Scenario: A metal-framed home in summer requires immediate cooling as outdoor temperatures rise.
- Inputs:
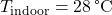 ,
,- Desired temperature range:
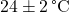 ,
, 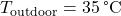 .
.- Calculation:
![Rendered by QuickLaTeX.com \[T_{\text{set}} = 28 - (28 - 24) = 24 \, \text{°C}.\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-773c5cfe2719eb2e54430c33d0d38f3b_l3.png)
- Outcome: The thermostat lowers the setpoint to 24 °C and activates cooling.
Python Code for Low Thermal Mass Algorithm
def adjust_setpoint(t_indoor, t_desired, tolerance, t_outdoor):
"""
Adjust the thermostat
setpoint dynamically for low thermal mass homes.
Parameters:
t_indoor (float): Current indoor temperature (°C).
t_desired (float): Desired indoor temperature (°C).
tolerance (float): Allowed temperature deviation (°C).
t_outdoor (float): Current outdoor temperature (°C).
Returns:
float: Adjusted thermostat setpoint (°C).
"""
if t_indoor < t_desired - tolerance:
return t_desired # Heating needed
elif t_indoor > t_desired + tolerance:
return t_desired # Cooling needed
else:
return t_indoor # No adjustment needed
# Example usage
setpoint = adjust_setpoint(t_indoor=28, t_desired=24, tolerance=2, t_outdoor=35)
print(f"Adjusted thermostat setpoint: {setpoint:.2f}°C")Seasonal Adjustments and Challenges
- Winter: Increased thermal lag due to lower solar radiation; preconditioning may require earlier start times.
- Summer: Faster thermal responses in low thermal mass homes necessitate more frequent dynamic adjustments.
- Moisture Content: Increased wall moisture in rainy seasons enhances thermal mass, slightly altering
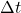 .
.
Summary of Thermostat Algorithms
- High thermal mass homes benefit from predictive preconditioning algorithms.
- Low thermal mass homes rely on real-time dynamic adjustments.
- Seasonal variations and material properties must be accounted for to refine the algorithms.
By implementing these algorithms and leveraging the provided Python code, homeowners can optimize their HVAC systems, reduce energy costs, and maintain consistent indoor comfort year-round.
11.2.1 Predictive Heating and Cooling Adjustments
Predictive heating and cooling adjustments aim to enhance HVAC system efficiency by leveraging thermal mass data, real-time indoor and outdoor conditions, and weather forecasts. These adjustments align HVAC operations with a building’s thermal inertia to optimize energy consumption while maintaining indoor comfort. Unlike real-time thermostat adjustments discussed in 11.1, this section focuses on system-wide predictive strategies using broader datasets and forecast information.
Key Concepts from 11.1
- Thermal Lag (
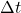 ):
):
As defined in 11.1,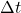 quantifies the delay between changes in outdoor conditions and their impact on indoor temperature. The equation for
quantifies the delay between changes in outdoor conditions and their impact on indoor temperature. The equation for 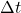 is:
is:
This thermal lag remains central to predictive models, dictating the timing of HVAC preconditioning.![Rendered by QuickLaTeX.com \[\Delta t = \frac{\rho \cdot c \cdot d^2}{k}\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-e64deabf1f887f84e83ad9f9453de7c3_l3.png)
- Preconditioning Start Time:
Preconditioning ensures that HVAC adjustments are initiated before significant temperature changes impact indoor conditions. This timing depends on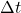 and is calculated as:
and is calculated as:
In 11.2, this is extended to include weather forecasts and multi-zone control.![Rendered by QuickLaTeX.com \[t_{\text{start}} = t_{\text{desired}} - \Delta t\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-8fa8d168e775a72ac85c324b1c4412b1_l3.png)
- Temperature Prediction:
Forecast-based temperature predictions use solar radiation ( ), outdoor temperature (
), outdoor temperature (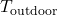 ), and material properties to estimate future indoor temperature (
), and material properties to estimate future indoor temperature (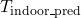 ):
): ![Rendered by QuickLaTeX.com \[T_{\text{indoor\_pred}}(t + \Delta t) = T_{\text{indoor}} + \frac{\left(T_{\text{outdoor}} - T_{\text{indoor}}\right) \cdot \Delta t}{\rho \cdot c \cdot d^2} + \frac{Q_{\text{solar}} \cdot A_{\text{window}}}{\rho \cdot c \cdot V}\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-91855c2782e45ee868ce44a773db8023_l3.png)
Integration of Forecast Data
In predictive HVAC adjustments, forecasted weather data adds a layer of intelligence, allowing the system to anticipate and adapt to future temperature changes. Key elements include:
- Outdoor Temperature Forecast (
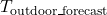 ):
):
- Captures expected temperature fluctuations over a specific period.
- Essential for scheduling preemptive heating or cooling.
- Solar Radiation Forecast (
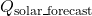 ):
):
- Predicts sunlight intensity at different times of the day.
- Critical for estimating passive heat gains in zones with high window exposure.
- Humidity Forecast:
- Outdoor humidity (
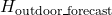 ) affects latent heat transfer and overall thermal comfort.
) affects latent heat transfer and overall thermal comfort.
Extended Use Case Examples
Example 1: Winter Heating for a High Thermal Mass Home
- Scenario: A brick-walled house must maintain 22 °C indoors during a cold winter morning.
- Inputs:
- Current indoor temperature (
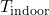 ): 18 °C,
): 18 °C, - Forecasted outdoor temperature (
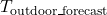 ): Drop from 5 °C to -3 °C,
): Drop from 5 °C to -3 °C, - Forecast duration: 8 hours,
- Material properties: Brick (
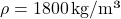 ,
, 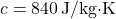 ,
, 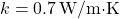 ,
, 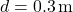 ),
), - Window area (
 ): 6 m²,
): 6 m², - Indoor volume (
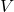 ): 200 m³,
): 200 m³, - Solar radiation forecast:
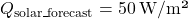 .
. - Calculation:
[
\Delta t = \frac{\rho \cdot c \cdot d^2}{k} = \frac{1800 \cdot 840 \cdot 0.3^2}{0.7} \approx 5.4 \, \text{hours}.
] Temperature prediction for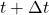 :
:
[
T_{\text{indoor_pred}} = 18 + \frac{\left(-3 – 18\right) \cdot 5.4}{5.4 + 1} + \frac{50 \cdot 6}{1800 \cdot 840 \cdot 200}.
] Predicted result: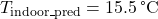 .
. - Outcome:
The system initiates heating 5.4 hours in advance to ensure indoor temperature does not drop below 22 °C.
Example 2: Summer Cooling for a Low Thermal Mass Home
- Scenario: A wooden house needs to maintain 24 °C indoors during a summer afternoon heatwave.
- Inputs:
- Current indoor temperature (
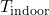 ): 27 °C,
): 27 °C, - Forecasted outdoor temperature (
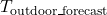 ): Rise from 30 °C to 38 °C,
): Rise from 30 °C to 38 °C, - Forecast duration: 6 hours,
- Material properties: Wood (
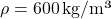 ,
, 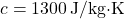 ,
, 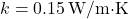 ,
, 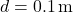 ),
), - Window area (
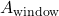 ): 4 m²,
): 4 m², - Solar radiation forecast:
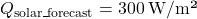 .
. - Calculation:
Temperature prediction for![Rendered by QuickLaTeX.com \[\Delta t = \frac{600 \cdot 1300 \cdot 0.1^2}{0.15} \approx 0.52 \, \text{hours}.\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-5a8f86a43f2e4af30c416eb82006e0a2_l3.png)
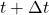 :
:
Predicted result:![Rendered by QuickLaTeX.com \[T_{\text{indoor\_pred}} = 27 + \frac{\left(38 - 27\right) \cdot 0.52}{0.52 + 0.5} + \frac{300 \cdot 4}{600 \cdot 1300 \cdot 4}.\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-8e67a43c86b9dbfda657d6276c450bf8_l3.png)
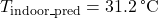 .
. - Outcome:
Cooling begins approximately 30 minutes before the forecasted heatwave to stabilize the indoor temperature.
Practical Implementation
- Sensor Placement Guidance:
- Outdoor Temperature Sensor:
- Place far from walls, roofs, or other surfaces that may radiate stored heat.
- Position in a shaded area to avoid direct sunlight.
- Indoor Temperature Sensors:
- Install centrally in each room or zone, avoiding direct airflow from vents.
- Solar Radiation Sensors:
- Mount on roofs or exposed areas where sunlight is unobstructed.
- Forecast Data Integration:
- Retrieve hourly weather forecasts using APIs from services like OpenWeatherMap.
- Align forecast data intervals with HVAC system operational cycles.
Challenges and Solutions
- Inconsistent Weather Data:
- Solution: Use moving averages to smooth forecast fluctuations.
- Limited Sensor Availability:
- Solution: Approximate solar gain using window orientation and cloud cover estimates.
- Seasonal Adjustments:
- Enhance thermal mass algorithms during winter to account for longer thermal lag.
Python Code for Predictive Adjustments
import math
def predict_indoor_temperature(t_indoor, t_outdoor, rho, c, thickness, conductivity, q_solar, window_area, volume):
"""
Predict future indoor temperature based on thermal properties and forecast data.
Parameters:
t_indoor (float): Current indoor temperature (°C).
t_outdoor (float): Forecasted outdoor temperature (°C).
rho (float): Material density (kg/m³).
c (float): Specific heat capacity (J/kg·K).
thickness (float): Material thickness (m).
conductivity (float): Thermal conductivity (W/m·K).
q_solar (float): Solar radiation (W/m²).
window_area (float): Window area (m²).
volume (float): Indoor space volume (m³).
Returns:
float: Predicted indoor temperature (°C).
"""
# Calculate thermal lag
delta_t = (rho * c * thickness**2) / conductivity
# Predict indoor temperature
t_indoor_pred = t_indoor + ((t_outdoor - t_indoor) * delta_t) / (delta_t + 1)
t_indoor_pred += (q_solar * window_area) /
(rho * c * volume)
return t_indoor_pred
# Example usage
predicted_temp = predict_indoor_temperature(
t_indoor=18, t_outdoor=-3, rho=1800, c=840, thickness=0.3, conductivity=0.7,
q_solar=50, window_area=6, volume=200
)
print(f"Predicted Indoor Temperature: {predicted_temp:.2f}°C")Summary
Predictive heating and cooling adjustments leverage thermal inertia and weather data for efficient HVAC scheduling. By combining the equations and strategies outlined in 11.1 with predictive models, homeowners can achieve optimal comfort while reducing energy costs. Implementing these adjustments ensures proactive HVAC operation, especially in challenging seasonal conditions.
11.2.2 Integrating Weather Forecast Data with Thermal Inertia
Integrating weather forecast data into HVAC scheduling allows predictive models to leverage thermal inertia while accounting for dynamic external environmental changes. This approach enhances the adaptability of the HVAC system, reducing energy usage while maintaining thermal comfort.
Where 11.1 focused on thermostat-level adjustments and 11.2.1 detailed predictive heating and cooling based on thermal inertia, 11.2.2 emphasizes the full integration of weather forecasts into HVAC decision-making processes, including practical implementation strategies, challenges, and advanced techniques for systems without solar radiation sensors.
Overview of Weather Forecast Data Integration
Weather forecast data introduces a temporal dimension to HVAC optimization, enabling the system to make anticipatory adjustments. This integration involves:
- Key Forecast Parameters:
- Temperature Forecast (
 ): Predicts future outdoor temperatures to anticipate heat gain/loss.
): Predicts future outdoor temperatures to anticipate heat gain/loss. - Solar Radiation Forecast (
 ): Estimates sunlight intensity and passive heat gain.
): Estimates sunlight intensity and passive heat gain. - Humidity Forecast (
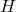 ): Affects the latent heat transfer and human comfort levels.
): Affects the latent heat transfer and human comfort levels. - Wind Speed and Direction: Impacts convective heat transfer across building surfaces.
- Temporal Resolution:
- Weather forecasts are typically available in hourly or daily intervals.
- HVAC systems use forecast windows aligned with the building’s thermal lag (
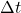 ).
).
- Adaptation to Seasonal Variations:
- Summer: Focus on pre-cooling during predicted heatwaves.
- Winter: Emphasis on pre-heating during forecasted cold spells.
Advanced Use Case Examples
Example 1: Winter Heating for a Multi-Zone System
- Scenario: A high thermal mass home with three zones must maintain different indoor temperatures during a week of fluctuating weather.
- Inputs:
- Zone 1 (Living Room):
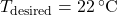 ,
, - Zone 2 (Bedrooms):
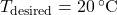 ,
, - Zone 3 (Kitchen):
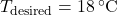 ,
, - Forecast: Daytime
 , nighttime
, nighttime  ,
, - Material: Brick walls (
 ),
), - Solar radiation forecast:
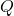 during the day.
during the day. - Steps:
- Thermal Lag Calculation for Each Zone:
Using Equation 1 from 11.1, calculate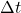 for each zone.
for each zone. - Temperature Prediction:
Apply the predictive heating model for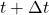 using the forecasted outdoor temperature and solar gain for each zone.
using the forecasted outdoor temperature and solar gain for each zone. - Preconditioning Scheduling:
Adjust HVAC start times for each zone to meet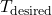 .
.
- Outcome:
- Zone 1 begins pre-heating at 5:00 AM to reach 22 °C by 8:00 AM.
- Zone 2 starts at 4:30 AM to reach 20 °C.
- Zone 3 remains passive due to its lower
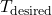 and higher thermal inertia.
and higher thermal inertia.
Example 2: Summer Cooling Without Solar Radiation Sensor
- Scenario: A low thermal mass home needs to cool efficiently during a predicted heatwave, but the system lacks a solar radiation sensor.
- Inputs:
- Current
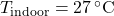 ,
, - Forecasted outdoor temperatures:
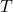 ,
, - Solar gain estimate: Window orientation suggests
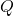 .
. - Steps:
- Approximation of
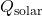 :
:
Estimate solar gain using geographic location, time of day, and cloud cover. - Predictive Cooling Adjustment:
Use the predicted indoor temperature equation from 11.2.1 to schedule cooling. - Dynamic Adjustments:
Monitor forecast changes to refine cooling schedules in real time.
- Outcome:
The system initiates cooling 15 minutes in advance, compensating for the lack of direct solar data with estimated values.
Challenges and Solutions
- Forecast Accuracy:
- Challenge: Short-term forecasts may deviate, leading to inefficiencies.
- Solution: Use rolling averages or integrate multiple forecast sources for redundancy.
- Lack of Sensors:
- Challenge: Solar radiation sensors may be unavailable in many systems.
- Solution: Approximate solar gain using orientation, shading, and historical data.
- Multi-Zone Synchronization:
- Challenge: Zones with different thermal properties require varied adjustments.
- Solution: Apply zone-specific thermal lag values and dynamically update schedules.
Seasonal Adjustments
- Winter:
- Longer thermal lags require earlier preconditioning.
- Passive solar heating can reduce heating loads during sunny days.
- Summer:
- Increased solar gain necessitates early cooling.
- Evening cooling schedules should consider delayed heat dissipation in high thermal mass homes.
Practical Implementation Guidelines
- Sensor Placement:
- Outdoor Temperature Sensors:
- Place at least 1.5 meters from walls or surfaces to minimize radiative heat effects.
- Ensure the sensor is shielded from direct sunlight and precipitation.
- Humidity Sensors:
- Outdoor sensors should be placed in ventilated enclosures.
- Indoor sensors must avoid proximity to humidifiers or heat sources.
- Forecast Data:
- Use APIs from services like OpenWeatherMap or AccuWeather to retrieve real-time and future weather data.
- Align data frequency (hourly or daily) with the HVAC system’s operational cycle.
Python Code: Full Integration of Forecast Data
import math
import requests
def get_weather_forecast(api_key, location):
"""
Fetches weather forecast data using OpenWeatherMap API.
Parameters:
api_key (str): API key for OpenWeatherMap.
location (str): Location for which forecast data is needed.
Returns:
dict: Parsed forecast data including temperature and solar estimates.
"""
url = f"http://api.openweathermap.org/data/2.5/forecast?q={location}&appid={api_key}&units=metric"
response = requests.get(url)
forecast_data = response.json()
parsed_data = {
"temp_forecast": [entry["main"]["temp"] for entry in forecast_data["list"]],
"solar_estimate": [200 if "clear" in entry["weather"][0]["description"].lower() else 50 for entry in forecast_data["list"]]
}
return parsed_data
def schedule_hvac(t_indoor, temp_forecast, q_solar_forecast, rho, c, thickness, conductivity, window_area, volume, delta_t):
"""
Predicts and schedules HVAC adjustments based on forecast data.
Parameters:
t_indoor (float): Current indoor temperature (°C).
temp_forecast (list): Forecasted outdoor temperatures (°C).
q_solar_forecast (list): Forecasted solar radiation values (W/m²).
rho (float): Material density (kg/m³).
c (float): Specific heat capacity (J/kg·K).
thickness (float): Material thickness (m).
conductivity (float): Thermal conductivity (W/m·K).
window_area (float): Window area (m²).
volume (float): Indoor volume (m³).
delta_t (float): Thermal lag (hours).
Returns:
list: Schedule of HVAC adjustments with timestamps.
"""
hvac_schedule = []
for i, t_outdoor in enumerate(temp_forecast):
t_indoor_pred = t_indoor + ((t_outdoor - t_indoor) * delta_t) / (delta_t + 1)
t_indoor_pred += (q_solar_forecast[i] * window_area) / (rho * c * volume)
if t_indoor_pred < 20: # Example: Maintain 20°C minimum
hvac_schedule.append((i, "Heat"))
elif t_indoor_pred > 25: # Example: Maintain 25°C maximum
hvac_schedule.append((i, "Cool"))
return hvac_schedule
# Example Usage
api_key = "your_api
_key_here"
location = "New York"
forecast = get_weather_forecast(api_key, location)
hvac_schedule = schedule_hvac(
t_indoor=22, temp_forecast=forecast["temp_forecast"],
q_solar_forecast=forecast["solar_estimate"], rho=1800, c=840,
thickness=0.3, conductivity=0.7, window_area=5, volume=250, delta_t=5
)
print(hvac_schedule)Summary
Integrating weather forecast data into HVAC systems enhances the predictive capability of thermal inertia models. By applying advanced forecasting techniques and practical implementation strategies, this approach ensures energy-efficient operation while maintaining comfort. Homeowners and automation enthusiasts can use these methods to build adaptive systems that thrive under varying climatic conditions.
11.3.1 Strategies for High Thermal Mass Homes
High thermal mass homes, built with materials like concrete, brick, or stone, retain heat or cold for longer durations due to their significant storage capacity. Automation strategies for such homes must account for their slow temperature response, making preconditioning and predictive adjustments critical for maximizing comfort and energy efficiency.
Characteristics of High Thermal Mass Homes
- Thermal Lag:
- Defined in 11.1, thermal lag (
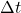 ) for high thermal mass homes is generally longer due to high heat capacity (
) for high thermal mass homes is generally longer due to high heat capacity ( ), density (
), density ( ), and material thickness (
), and material thickness ( ).
). - Predictive adjustments must begin hours before the desired indoor temperature change.
- Slow but Steady Temperature Changes:
- These homes are resistant to sudden outdoor temperature fluctuations, providing inherent stability.
- Optimal for regions with significant diurnal temperature variations.
- Dependency on Solar Gains:
- Passive solar heating contributes significantly to temperature maintenance.
- Requires careful integration of solar radiation data or approximations if sensors are unavailable.
Use Case Examples
Example 1: Winter Pre-Heating with Zone-Specific Requirements
- Scenario:
A family home with high thermal mass materials requires efficient heating during a cold winter evening. - Inputs:
- Material: Brick (
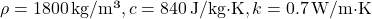 ),
), - Wall thickness (
 ): 0.3 m,
): 0.3 m, - Desired indoor temperature:
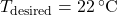 ,
, - Forecasted outdoor temperature:
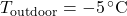 .
. - Steps:
- Calculate
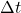 :
:
Using Equation 1 from 11.1, calculate the thermal lag.![Rendered by QuickLaTeX.com \[\Delta t = \frac{\rho \cdot c \cdot d^2}{k} = \frac{1800 \cdot 840 \cdot 0.3^2}{0.7} \approx 5.4 \, \text{hours}.\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-84c8ea3f46b6156fa29623af8f4ece5d_l3.png)
- Predict Indoor Temperature Shift:
Apply the predictive temperature equation from 11.2 to determine when to begin heating. - Adjust HVAC Schedule:
Start heating approximately 5.4 hours earlier to compensate for the thermal lag.
- Outcome:
The system reaches the desired temperature at 6:00 PM by starting pre-heating at 12:30 PM.
Example 2: Passive Cooling During Summer Afternoons
- Scenario:
A south-facing home with large windows experiences high solar gain but leverages its thermal mass to remain cool. - Inputs:
- Solar radiation forecast:
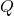 ,
, - Current indoor temperature:
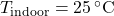 ,
, - Forecasted outdoor temperature:
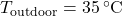 .
. - Steps:
- Use Shading or Reflective Coatings:
Reduce solar gain by 50% using curtains or coatings. - Optimize Window Openings:
Open windows during cool nights to dissipate heat stored in the mass. - Delay HVAC Operation:
Predict when the indoor temperature will exceed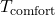 and initiate cooling later.
and initiate cooling later.
- Outcome:
Energy savings are achieved by delaying cooling until passive measures are exhausted.
Algorithm for High Thermal Mass Homes
The automation algorithm for high thermal mass homes prioritizes early HVAC adjustments. It uses the equations and thermal properties outlined in 11.1 and 11.2, with additional consideration for zones, shading, and solar gain.
Python Implementation
def high_mass_hvac_schedule(t_indoor, t_outdoor_forecast, q_solar_forecast, rho, c, thickness, conductivity, window_area, volume, delta_t, t_desired):
"""
HVAC scheduling for high thermal mass homes using predictive algorithms.
Parameters:
- t_indoor (float): Current indoor temperature (°C).
- t_outdoor_forecast (list): Forecasted outdoor temperatures (°C).
- q_solar_forecast (list): Solar radiation forecast (W/m²).
- rho (float): Material density (kg/m³).
- c (float): Specific heat capacity (J/kg·K).
- thickness (float): Material thickness (m).
- conductivity (float): Thermal conductivity (W/m·K).
- window_area (float): Window area (m²).
- volume (float): Indoor volume (m³).
- delta_t (float): Thermal lag (hours).
- t_desired (float): Desired indoor temperature (°C).
Returns:
list: Schedule of HVAC adjustments.
"""
schedule = []
for i, t_outdoor in enumerate(t_outdoor_forecast):
t_pred = t_indoor + ((t_outdoor - t_indoor) * delta_t) / (delta_t + 1)
t_pred += (q_solar_forecast[i] * window_area) / (rho * c * volume)
if t_pred < t_desired:
schedule.append((i, "Heat"))
elif t_pred > t_desired + 2: # Example: Comfort range
schedule.append((i, "Cool"))
return schedule11.3.2 Strategies for Low Thermal Mass Homes
Low thermal mass homes, often constructed with materials like wood or lightweight materials, exhibit rapid indoor temperature changes in response to outdoor fluctuations. Automation strategies for such homes focus on dynamic, real-time adjustments for heating and cooling.
Characteristics of Low Thermal Mass Homes
- Minimal Thermal Lag:
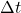 is significantly shorter compared to high thermal mass homes, as calculated using Equation 1.
is significantly shorter compared to high thermal mass homes, as calculated using Equation 1.- Real-time data becomes critical.
- Rapid Temperature Fluctuations:
- These homes cannot buffer temperature changes, requiring frequent HVAC interventions.
- Impact of Insulation:
- Adding insulation can reduce heat exchange but does not fundamentally alter thermal lag.
Use Case Examples
Example 1: Real-Time Heating During Cold Nights
- Scenario:
A low thermal mass cabin in a mountain region faces sudden temperature drops at night. - Inputs:
 ,
,- Forecasted outdoor temperatures:
 ,
, - Wall material: Wood (
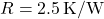 ).
). - Steps:
- Monitor Forecast Data:
Use hourly outdoor temperature forecasts. - Dynamic Adjustment:
Initiate heating immediately when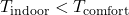 .
.
- Outcome:
Frequent but energy-efficient heating cycles maintain comfort.
Algorithm for Low Thermal Mass Homes
Dynamic control is emphasized for low thermal mass homes. The system continuously monitors conditions and adjusts HVAC settings in real time.
Python Implementation
def low_mass_hvac_control(t_indoor, t_outdoor_forecast, comfort_range):
"""
Real-time HVAC control for low thermal mass homes.
Parameters:
- t_indoor (float): Current indoor temperature (°C).
- t_outdoor_forecast (list): Forecasted outdoor temperatures (°C).
- comfort_range (tuple): Desired indoor temperature range (min, max).
Returns:
list: Dynamic HVAC actions based on forecast.
"""
actions = []
for t_outdoor in t_outdoor_forecast:
if t_indoor < comfort_range[0]:
actions.append("Heat")
elif t_indoor > comfort_range[1]:
actions.append("Cool")
else:
actions.append("Maintain")
return actionsKey Differences and Recommendations
- Thermal Response:
- High thermal mass: Gradual adjustments.
- Low thermal mass: Rapid, real-time actions.
- Integration:
- High thermal mass homes benefit from predictive scheduling.
- Low thermal mass homes require real-time sensors and minimal reliance on forecasts.
- Practical Recommendations:
- High thermal mass: Focus on preconditioning and solar gain.
- Low thermal mass: Prioritize fast-acting HVAC systems and insulation improvements.
Final Recommendations
Homeowners can use the algorithms and examples provided to build tailored automation strategies for their specific thermal inertia properties. For mixed-material homes, hybrid strategies should be considered
11.4 Advanced Integration of Thermal Inertia into Smart Home Systems
As smart home systems grow increasingly sophisticated, the integration of thermal inertia into comprehensive automation strategies becomes essential for optimizing energy efficiency, comfort, and cost savings. Part 11.4 delves into advanced integration techniques for thermal inertia management, focusing on multi-zone systems, hybrid thermal inertia scenarios, and dynamic integration with renewable energy systems.
11.4.1 Multi-Zone Management of Thermal Inertia
Multi-zone management involves customizing thermal inertia strategies for different areas or rooms within a home. This is critical for larger homes or buildings where thermal inertia and usage patterns vary significantly across zones.
Key Concepts
- Zone-Specific Thermal Characteristics:
- Each zone may have distinct thermal properties based on its material composition, insulation, and exposure to sunlight.
- Example: A south-facing living room with large windows will have higher solar gain than a north-facing bedroom.
- Variable Occupancy and Usage:
- Zonal control must consider occupancy schedules. A home office used only during the day will have different requirements from a bedroom primarily used at night.
- Independent HVAC Controls:
- Advanced HVAC systems with independent zone control can optimize energy usage by heating or cooling only occupied zones.
Algorithm for Multi-Zone Thermal Management
This algorithm integrates zone-specific thermal inertia parameters and occupancy schedules for efficient control.
Steps:
- Define Zone Properties:
- Input zone-specific data such as material type, thermal lag, and dimensions.
- Example:
- Living Room: High thermal mass, large windows, high solar gain.
- Bedroom: Low thermal mass, small windows, low solar gain.
- Incorporate Occupancy Data:
- Use occupancy sensors or predefined schedules to prioritize active zones.
- Adjust HVAC Settings per Zone:
- Apply predictive or real-time algorithms (see 11.1 and 11.2) to each zone independently.
Example
Scenario: A two-zone home with a high-thermal-mass living room and a low-thermal-mass bedroom requires separate HVAC schedules.
- Inputs:
- Zone 1 (Living Room): Brick walls (
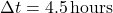 ), solar radiation forecast:
), solar radiation forecast: 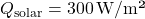 .
. - Zone 2 (Bedroom): Wood walls (
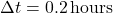 ), low solar gain.
), low solar gain.
- Steps:
- Preheat the living room starting at 6:30 AM to reach 21 °C by 11:00 AM.
- Dynamically adjust the bedroom temperature to maintain 20 °C between 9:00 PM and 7:00 AM.
# Python Implementation
def multi_zone_hvac(zones, occupancy_schedule, forecast_data):
"""
Multi-zone HVAC management based on thermal inertia and occupancy.
Parameters:
- zones (dict): Zone-specific properties (thermal lag, solar gain, etc.).
- occupancy_schedule (dict): Active hours for each zone.
- forecast_data (dict): Forecasted temperatures and solar radiation.
Returns:
dict: HVAC schedules for each zone.
"""
hvac_schedules = {}
for zone, properties in zones.items():
schedule = []
for hour, occupancy in enumerate(occupancy_schedule[zone]):
if occupancy:
t_pred = predict_temperature(properties, forecast_data[hour])
if t_pred < properties["desired_temp"]:
schedule.append((hour, "Heat"))
elif t_pred > properties["desired_temp"] + 2:
schedule.append((hour, "Cool"))
hvac_schedules[zone] = schedule
return hvac_schedulesChallenges and Recommendations
- Sensor Placement:
- Place indoor sensors in central locations within each zone, avoiding direct sunlight or drafts.
- Use additional sensors for zones with uneven temperature distribution.
- Coordination of HVAC Systems:
- Ensure that multi-zone systems do not conflict, particularly in shared air circulation setups.
- Energy Efficiency:
- Use zone prioritization to focus resources on high-usage areas.
11.4.2 Hybrid Thermal Inertia Scenarios
In real-world scenarios, homes often have a mix of high and low thermal mass materials. This section explores hybrid strategies to manage such cases effectively.
Key Concepts
- Mixed Thermal Properties:
- A single zone may contain both high and low thermal mass elements.
- Example: A living room with concrete walls (high thermal mass) and large glass windows (low thermal mass).
- Dynamic Switching Between Strategies:
- Systems must dynamically switch between predictive (for high thermal mass) and real-time (for low thermal mass) strategies.
- Integration with Renewable Energy:
- Hybrid systems can leverage renewable energy sources, such as solar panels, for heating or cooling high thermal mass zones during surplus generation periods.
Algorithm for Hybrid Thermal Inertia Management
This algorithm combines predictive and real-time control methods for hybrid zones.
Example
Scenario: A hybrid living room with concrete walls and large glass windows.
- Inputs:
- Wall material: Concrete (
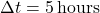 ).
). - Window material: Glass (
 ).
).
- Steps:
- Preheat concrete walls using predictive algorithms starting at 6:00 AM.
- Use dynamic adjustments to mitigate heat loss through windows in real time.
Challenges and Recommendations
- Synchronization:
- Coordinate heating and cooling actions to avoid redundancy.
- Energy Storage:
- Use high thermal mass zones as energy storage buffers during renewable energy surplus periods.
- System Calibration:
- Regularly calibrate sensors and algorithms for optimal performance.
Conclusion
By integrating multi-zone and hybrid thermal inertia strategies, smart home systems can achieve unprecedented levels of efficiency and comfort. Homeowners and developers are encouraged to experiment with the provided algorithms and adapt them to their specific needs.
11.5 Integrating Advanced Control Algorithms in Smart Home Systems
This section synthesizes the principles from Parts 11.1, 11.2, 11.3, and 11.4 and illustrates how advanced control algorithms like PID controllers can be implemented in smart home systems. By integrating concepts of thermal inertia, HVAC optimization, and sensor-based control, this section provides comprehensive guidance on achieving energy efficiency and indoor comfort.
11.5.1 Proportional-Integral-Derivative (PID) Control for Temperature Stabilization
PID control is an effective strategy for dynamically managing HVAC systems in response to indoor and outdoor conditions. Incorporating thermal inertia, weather data, and HVAC dynamics into PID controllers ensures a tailored approach for different types of homes.
Overview of PID Control
The PID controller calculates the control signal (![]() ) to drive the system toward the desired temperature (
) to drive the system toward the desired temperature (![]() ):
):
![]()
where:
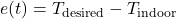 : Temperature error at time
: Temperature error at time 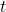 .
.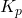 : Proportional gain.
: Proportional gain.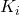 : Integral gain.
: Integral gain.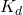 : Derivative gain.
: Derivative gain.
Incorporating Thermal Inertia
Thermal inertia affects how indoor temperature responds to heating or cooling. For high thermal inertia homes, HVAC adjustments must be slower and anticipatory, requiring lower ![]() ,
, ![]() , and
, and ![]() . Conversely, low thermal inertia homes necessitate faster, more reactive adjustments.
. Conversely, low thermal inertia homes necessitate faster, more reactive adjustments.
Integrating Findings from Previous Sections
- Part 11.1 Integration:
- Use adaptive scheduling principles to estimate thermal lag (
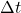 ) based on building materials.
) based on building materials. - Incorporate
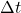 into the PID control signal for anticipatory adjustments in high thermal inertia homes.
into the PID control signal for anticipatory adjustments in high thermal inertia homes.
- Part 11.2 Integration:
- Leverage weather forecast data to modify PID control parameters dynamically. For instance, forecasted outdoor temperatures and solar radiation can be included in the
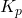 and
and 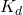 tuning.
tuning.
- Part 11.3 Integration:
- Use distinct strategies for high and low thermal inertia homes when tuning
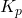 ,
, 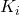 , and
, and 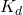 .
. - High thermal mass homes require preconditioning; low thermal mass homes depend on real-time adjustments.
- Part 11.4 Integration:
- Apply energy efficiency optimization principles by minimizing HVAC overshoot and energy waste using derivative control.
PID Tuning for Homes with High and Low Thermal Inertia
| Parameter | High Thermal Inertia | Low Thermal Inertia |
|---|---|---|
| 1–5 (low gain to prevent overshoot) | 5–15 (higher gain for rapid response) | |
| 0.01–0.1 (slow integral action) | 0.1–1 (faster integral action) | |
| 0.01–0.1 (to smooth responses) | 0.1–0.5 (to stabilize rapid changes) |
Sources:
- Åström, K. J., & Hägglund, T. (1995). PID Controllers: Theory, Design, and Tuning.
- López, G. et al. (2016). “Optimized PID Tuning for HVAC Systems with Thermal Inertia.”
Determining 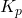 ,
, 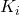 , and
, and 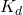 Experimentally
Experimentally
Step-by-Step Process:
- Proportional Gain (
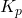 ):
):
- Set
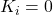 and
and 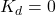 .
. - Gradually increase
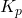 until the system oscillates stably around the setpoint. This value is the critical proportional gain (
until the system oscillates stably around the setpoint. This value is the critical proportional gain (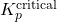 ).
).
- Integral Gain (
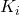 ):
):
- Use the critical
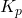 value.
value. - Increase
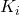 gradually until the system eliminates steady-state error without significant overshoot.
gradually until the system eliminates steady-state error without significant overshoot.
- Derivative Gain (
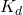 ):
):
- Fix
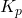 and
and 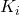 .
. - Adjust
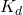 to reduce overshoot and smooth responses to rapid changes.
to reduce overshoot and smooth responses to rapid changes.
Python Implementation
Below is a Python script that integrates thermal inertia, weather forecasts, and sensor data into PID control.
from simple_pid import PID
import numpy as np
import matplotlib.pyplot as plt
# Hypothetical thermal response incorporating inertia and solar radiation
def thermal_response(control_signal, solar_radiation, thermal_mass):
"""Simulates indoor temperature change."""
return (control_signal - solar_radiation * 0.01) / thermal_mass
# Simulate PID-controlled HVAC system
def simulate_pid(Kp, Ki, Kd, T_desired, T_initial, solar_radiation, thermal_mass, steps):
pid = PID(Kp, Ki, Kd, setpoint=T_desired)
temperature = T_initial
temp_history = [temperature]
for step in range(steps):
control_signal = pid(temperature)
temperature += thermal_response(control_signal, solar_radiation[step], thermal_mass)
temp_history.append(temperature)
return temp_history
# Parameters
Kp, Ki, Kd = 3.0, 0.1, 0.05
T_desired = 22.0
T_initial = 18.0
thermal_mass = 0.8
steps = 500
solar_radiation = np.linspace(100, 400, steps)
# Run simulation
temperatures = simulate_pid(Kp, Ki, Kd, T_desired, T_initial, solar_radiation, thermal_mass, steps)
# Plot
plt.plot(temperatures)
plt.axhline(T_desired, color="red", linestyle="--", label="Desired Temperature")
plt.xlabel("Time Steps")
plt.ylabel("Temperature (°C)")
plt.title("PID-Controlled HVAC with Solar Radiation")
plt.legend()
plt.show()Challenges and Recommendations
- Sensor Integration:
- Outdoor sensors should be placed at least 2–3 meters from walls and shielded from direct sunlight.
- Indoor sensors should be centrally located and away from windows or HVAC vents.
- Thermal Lag:
- For high thermal inertia homes, include thermal lag (
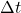 ) in control logic.
) in control logic.
- Seasonal Adjustments:
- In winter, increase
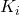 for slower heating needs.
for slower heating needs. - In summer, increase
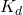 for stabilizing rapid cooling demands.
for stabilizing rapid cooling demands.
Conclusion
By synthesizing control strategies from PID methods with the principles of thermal inertia, smart home systems can achieve both comfort and efficiency. Integrating data-driven approaches with traditional control ensures adaptability to modern demands.
Conclusion
Thermal inertia represents a pivotal factor in advancing home automation systems, enabling smarter, more energy-efficient, and comfortable living environments. By seamlessly integrating the principles of thermal inertia with modern smart home technologies, homeowners can optimize energy use, enhance indoor comfort, and reduce environmental impact.
Key Contributions to Home Automation
- Smarter HVAC Systems:
The application of thermal inertia in home automation empowers HVAC systems to operate predictively and dynamically. By leveraging thermal mass, real-time heat storage capacity calculations, and weather forecasts, automated climate control systems can anticipate temperature changes and adjust operations efficiently. - Energy Efficiency Through Automation:
Automated systems that account for thermal inertia reduce unnecessary energy consumption by aligning HVAC schedules with the thermal properties of a home. High thermal mass materials enable homes to store and release heat naturally, while smart algorithms adjust heating or cooling cycles to minimize waste. - Real-Time Adaptation:
Advanced automation technologies, such as smart thermostats and machine learning models, enable real-time responses to changing conditions. These systems utilize sensor data, occupancy patterns, and environmental forecasts to maintain comfort while minimizing energy usage. - Customization and Scalability:
Home automation systems incorporating thermal inertia are highly customizable. Whether for high thermal mass homes requiring anticipatory preconditioning or low thermal mass homes needing rapid adjustments, these solutions adapt to a variety of building types, climates, and user preferences. - Sustainability and Smart Living:
By automating climate control with thermal inertia principles, smart homes can significantly reduce their carbon footprint. Integration with renewable energy sources, such as solar panels, further enhances sustainability, making these systems not only efficient but also eco-conscious.
Transforming Home Automation Through Thermal Inertia
The integration of thermal inertia into home automation signifies a shift toward intelligent and sustainable living. By combining the scientific principles of thermal inertia with cutting-edge automation technologies, homeowners gain control over their indoor climates with unprecedented precision. These systems not only save energy but also improve comfort and adapt seamlessly to seasonal variations.
As automation continues to evolve, the potential for thermal inertia in smart homes will expand, creating opportunities for enhanced user experiences, greater energy savings, and reduced environmental impact. This guide equips readers with the tools, algorithms, and practical knowledge to implement these strategies effectively.
By embracing thermal inertia, homeowners take a step toward the future of home automation—one that balances innovation, comfort, and sustainability. Together, these advancements set the stage for smarter, greener, and more adaptive living spaces that cater to the needs of both people and the planet.
Algorithm: Dynamic Home Heating and Cooling with Thermal Inertia
Inputs:
- Home’s thermal inertia parameters:
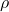 : Material density (kg/m³)
: Material density (kg/m³) : Specific heat capacity (J/kg·K)
: Specific heat capacity (J/kg·K)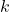 : Thermal conductivity (W/m·K)
: Thermal conductivity (W/m·K)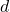 : Material thickness (m)
: Material thickness (m)- Sensor availability:
- Indoor temperature sensor (
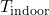 )
) - Outdoor temperature sensor (
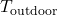 )
) - Solar radiation sensor (
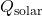 )
) - Occupancy sensor
- Desired temperature range:
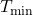 : Minimum acceptable temperature
: Minimum acceptable temperature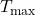 : Maximum acceptable temperature
: Maximum acceptable temperature- Heating/cooling system characteristics:
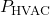 : Power of the HVAC system (W)
: Power of the HVAC system (W) : Efficiency of the HVAC system
: Efficiency of the HVAC system- Weather forecast data (if available)
Steps:
1. Initialization
- Identify available sensors.
- Retrieve or set home-specific thermal inertia parameters.
- For unavailable sensors:
- Estimate
 based on the time of day, season, and geographic location using: [ Q_{\text{solar_estimate}} = I \cdot A_{\text{window}} \cdot \tau_{\text{window}} ] where:
based on the time of day, season, and geographic location using: [ Q_{\text{solar_estimate}} = I \cdot A_{\text{window}} \cdot \tau_{\text{window}} ] where: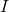 : Solar irradiance (W/m², typical values range from 100–1000 W/m²)
: Solar irradiance (W/m², typical values range from 100–1000 W/m²)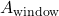 : Window area (m²)
: Window area (m²)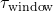 : Transmissivity of window glass (dimensionless, usually 0.5–0.9).
: Transmissivity of window glass (dimensionless, usually 0.5–0.9).
2. Sensor Data Collection
- Indoor Temperature (
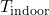 ):
):
- Retrieve real-time sensor data if available.
- If unavailable, estimate using thermal lag and outdoor temperature:
![Rendered by QuickLaTeX.com \[T_{\text{indoor}}(t) = T_{\text{outdoor}}(t-\Delta t) + \frac{Q_{\text{solar}} \cdot \Delta t}{\rho \cdot c \cdot d}\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-b4564655284f3c513d13f72c016bb094_l3.png)
- Outdoor Temperature (
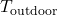 ):
):
- Retrieve from sensors or weather forecasts.
- Solar Radiation (
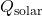 ):
):
- Use sensor data or estimate as detailed in Step 1.
- Occupancy:
- Retrieve real-time data or use default schedules.
3. Thermal Lag Estimation
- Calculate the thermal lag (
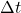 ) using:
) using:![Rendered by QuickLaTeX.com \[\Delta t = \frac{\rho \cdot c \cdot d^2}{k}\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-e64deabf1f887f84e83ad9f9453de7c3_l3.png)
Adjust dynamically if solar gain or occupancy significantly impacts heat transfer.
4. Heating/Cooling Adjustment Logic
Heating:
- If
 :
:
- Calculate heating start time using:
![Rendered by QuickLaTeX.com \[t_{\text{start}} = t_{\text{desired}} - \Delta t\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-8fa8d168e775a72ac85c324b1c4412b1_l3.png)
- Adjust for solar radiation to reduce heating load:
![Rendered by QuickLaTeX.com \[P_{\text{heating}} = \frac{\rho \cdot c \cdot V \cdot (T_{\text{min}} - T_{\text{indoor}})}{\eta_{\text{HVAC}}} - Q_{\text{solar}} \cdot A_{\text{window}}\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-3a320014bdfc11342983756232354342_l3.png)
where:
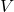 : Indoor volume (m³).
: Indoor volume (m³).
Cooling:
- If
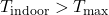 :
:
- Calculate cooling start time using:
![Rendered by QuickLaTeX.com \[t_{\text{start}} = t_{\text{desired}} - \Delta t\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-8fa8d168e775a72ac85c324b1c4412b1_l3.png)
- Anticipate heat gain and adjust cooling schedule:
![Rendered by QuickLaTeX.com \[P_{\text{cooling}} = \frac{\rho \cdot c \cdot V \cdot (T_{\text{indoor}} - T_{\text{max}})}{\eta_{\text{HVAC}}} + Q_{\text{solar}} \cdot A_{\text{window}}\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-ecdb89ad62d42cd2dcd1f3763055a620_l3.png)
5. Energy Optimization
- Leverage time-of-use energy pricing:
- Schedule heating/cooling during off-peak hours.
- Precondition the home using thermal inertia:
where:![Rendered by QuickLaTeX.com \[ E_{\text{stored}} = \rho \cdot c \cdot V \cdot \Delta T \]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-cde5c6d964fb2525ec5830ae08912c5d_l3.png)
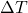 : Temperature difference achieved during preconditioning.
: Temperature difference achieved during preconditioning.
6. Occupancy-Based Overrides
- If occupancy detected:
- Maintain
![Rendered by QuickLaTeX.com T_{\text{indoor}} \in [T_{\text{min}}, T_{\text{max}}]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-2124676532d830c0063e76c8460ace60_l3.png) .
.
- If no occupancy detected for
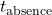 :
:
- Allow
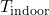 to drift:
to drift:![Rendered by QuickLaTeX.com \[T_{\text{drift}} = T_{\text{outdoor}} + \frac{Q_{\text{solar}} \cdot \Delta t}{\rho \cdot c \cdot d}\]](https://sensorpoweredhome.com/wp-content/ql-cache/quicklatex.com-39f0bea2f13952c2076065c492255d2a_l3.png)
7. System Update Loop
- Recalculate all inputs every 15 minutes:
- Update
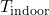 ,
, 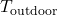 , and
, and 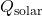 .
.
- Reassess
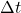 if significant weather or occupancy changes occur.
if significant weather or occupancy changes occur.
8. Output
- Generate HVAC commands:
- Start/stop heating or cooling.
- Adjust setpoints dynamically.
- Log actions and data for future optimization.
Notes for Implementation:
- For readers without sensors, default values and simple approximations are included to estimate critical inputs.
- Use software like Python for automation with libraries like
numpyfor numerical calculations andmatplotlibfor data visualization.
